Melléksodor

Non-mainstream

Tényleg a véletlen irányítja a világot?

2016. augusztus 03. 00:23 - Csebó Horváth János

Bevezetés

A manapság uralkodó materialista világnézet szerint a világ működése véletlenszerű. Eszerint ugyanis:

  • a világ véletlenszerűenkeletkezett a semmiből
  • az Univerzum jelenleg megfigyelhető struktúrája véletlenszerűen alakult ki az anyag egy alacsonyan strukturált állapotából
  • az élő organizmusok véletlenszerűenjöttek létre az élettelen anyagból
  • az öntudattal bíró ember véletlenszerűenfejlődött ki a primitív élő organizmusokból.

Vajon mikor és miként lett a véletlenszerűség elve a világ jelenségeinek domináns magyarázó elve? A kérdés annál is indokoltabb, mert a XIX. század végéig ezt a magyarázó szerepet inkább az okság elve töltötte be. Az oksági elv a determinisztikus világkép magyarázó elve, a véletlenszerűség pedig az indeterminisztikus világképnek felel meg. Alapkérdésünk a következő: mikor, hogyan és miért váltotta fel az indeterminizmus a determinizmus dominanciáját a világ jelenségeinek értelmezésében? A „mikor” és a „hogyan” válaszhoz mindenekelőtt a XX. század elején megszületett kvantumelmélet történetét kell megnéznünk, a „miért” viszont, mint majd látni fogjuk, ennél még messzebb vezet.

A Wikipédiának a fentebb már hivatkozott determinizmus szócikke is mutatja, hogy a kvantumelmélettel kell foglalkoznunk, itt ugyanis a következőt olvashatjuk: „A kvantumelmélet szerint a világ működése nem determinisztikus, a részecskék mozgását ugyanis determinisztikus törvények helyett a hullámfüggvény írja le, ami a részecskék mozgására csak valószínűségi jóslatokat ad.” Ha elfogadjuk, hogy ez a szócikk a közvélemény egy részének a véleményét fejezi ki, meg kell vizsgálnunk, hogy magából a kvantumelméletből következik-e, hogy a világ működése nem determinisztikus?

Látni fogjuk, hogy a világ működése valójában a kvantumelméletnek csak az egyik interpretációja szerint indeterminisztikus, és hogy lehetséges az elmélet determinisztikus interpretációja is. Az igaz, hogy az indeterminisztikus interpretáció a legismertebb, de az már nem igaz, hogy ez az értelmezés felelne meg legjobban a tapasztalatoknak. Létezik olyan determinisztikus értelmezés is, amely ugyanúgy összhangban van minden tapasztalattal, mint az indeterminisztikus. Akkor vajon mi az oka az indeterminisztikus interpretáció dominanciájának? Többek között erre a kérdésre keressük a választ ebben a dolgozatban. Ehhez azonban meg kell nézzük, hogyan vetődött fel az indeterminizmus kérdése már a kvantummechanika kezdeteinél és milyen válaszokat adhatunk ma ezekre a kérdésekre?

A Heisenberg-féle határozatlansági reláció levezetése

 

A szélesebb közvélemény előtt is ismert, hogy a kvantumelmélet alapvető fogalma a Heisenberg-féle határozatlansági reláció, ezért először azzal fogunk megismerkedni.

A könnyebb érthetőség kedvéért egy, a hétköznapokból is jól ismert jelenséggel kezdünk. Először azt nézzük meg, hogyan viselkednek a vízhullámok, ha az útjukat elzárjuk és csak egy résen engedjük át őket. Ekkor a hullámok egyik jellemző tulajdonságát, az elhajlást tapasztalhatjuk: a hullámok a rés két széle által árnyékolt területen is megjelennek. „Csökkentve a rés szélességét, egyre erősebben eltérnek a hullámok az eredeti terjedési iránytól az akadály szélén. Egészen szűk nyílást alkalmazva jól látható, hogy a rés utáni hullám olyan, mintha a rés helyén keltették volna egy pontszerű hullámkeltővel.”

            

Az alábbi képen a vízhullámok interferenciáját látjuk. (A linkre kattintva egy szemléletesebb mozgó filmet láthatunk.) Ha két vagy több hullám találkozik, a hullámok egyes helyeken erősítik, más helyeken pedig gyengítik egymást: ez az interferencia jelensége. Az alábbi képen láthatjuk, hogy több hullám elindulása után néhány irányban gyengült a hullámzás ereje, más irányokban pedig nem.

Az elektronnal végzett kísérletek eredményei már a XIX. század végétől azt sugallták, hogy a tapasztalatok értelmezését a makroszkopikus hullámjelenségekkel analóg módon végezzék. Az alábbi ábrán látható kísérletben az elektronok becsapódásakor a fluoreszkáló ernyőn ugyanis ahhoz hasonló gyűrűk jönnek létre, mint amit a vízhullámok interferenciájánál látunk. (Az itteni gyűrűk az előző képen látható sugaraknak felelnek meg.)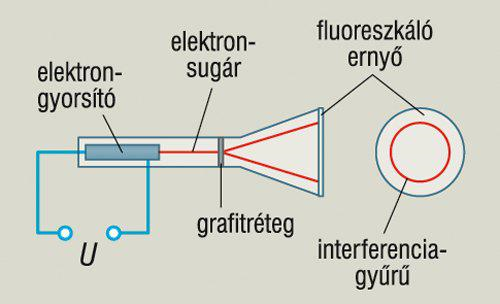

Ez az analógia sugallt a kvantummechanika felfedezői számára egy, az alábbi ábrán láthatóhoz hasonló gondolatkísérletet, amiből aztán a határozatlansági relációt levezették. Az ábrán egy olyan kísérlet sémája látható, amikor egy mozgó elektronnyalábot engedünk át egy kis, dx szélességű résen. (Forrás: fizika.mechatronika.hu/fizika/fizikalecok/Új%20mappa/hhr.doc) 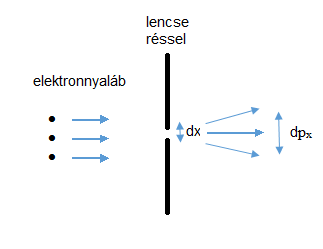A réstől eltávolodó elektron x koordinátáját nem ismerhetjük a rés szélességénél (dx) pontosabban. Ha a rést szűkítjük, akkor csökken a hely bizonytalansága, de jobban szétterül a hullám (Vö. elhajlás). A szétterülésből az következik, hogy ha szűkítjük a rést, hogy pontosabban ismerjük az elektron helyét, akkor egyre nagyobb lesz az elektron impulzusa x koordinátájának, vagyis a px –nek a dpx bizonytalansága.

Heisenberg hasonló megfontolások és kísérleti tapasztalatok alapján jutott arra a következtetésre, hogy egy részecske helye és impulzusa egyszerre nem határozható meg tetszőleges pontossággal. A két adat bizonytalanságának szorzata egy bizonyos értéknél nem lehet kisebb, ha csökkentjük az egyiket, akkor a másiknak növekednie kell. A mérések szerint a következő összefüggés áll fenn:

dx * dpx ≥ ħ/2 ,

ahol a ħ egy univerzális fizikai állandó, az úgynevezett redukált Planck-állandó. Nézzük, hogyan értelmezte Heisenberg a fenti, róla elnevezett egyenlőtlenséget.

„Lehet ugyan az elektron helyéről és sebességéről beszélni, mint a newtoni mechanikában, mindkettőt megfigyelhetjük vagy mérhetjük. De nem lehet mindkét mennyiséget egyidejűleg tetszőleges pontossággal meghatározni.” (Werner Heisenberg, 86). (Látjuk, hogy Heisenberg a sebességről beszél az impulzus helyett. Ezt azért teheti, mert az impulzus a sebességgel arányos mennyiség, p = m*v, ahol az m a tömeg. Kis sebességek esetén a tömeg állandónak tekinthető, így az impulzus helyett nyugodtan mondhatunk sebességet.)

És ezzel már el is érkeztünk az indeterminizmus kérdéséhez: a makroszkopikus világban érvényes klasszikus mechanika szerint ugyanis, ha egyidejűleg ismerjük egy test helyét és sebességét egy tetszőleges pillanatban, akkor abból előre meg tudjuk határozni a helyét a jövő egy tetszőleges pillanatában. Erre mondjuk, hogy a makroszkopikus testek mozgása determinált. Ennek köszönhető többek között, hogy egy nyílvesszővel le tudjuk lőni a vadat, mert emiatt tudjuk kiszámolni, hogy hol lesz a vad, mire a kilőtt nyílvessző odaér a vad közelébe. Ezt tehát az alapján tudjuk megtenni, hogy látjuk a vadat, így tudjuk, hogy egy adott pillanatban hol van és ezzel egy időben fel tudjuk mérni a sebességét, amiből megbecsüljük, hogy mikor lesz azon a helyen, ahova a mi nyílvesszőnk elérhet. A Heisenberg-féle reláció szerint viszont a mikroszkopikus világban erre nincs lehetőségünk, az elektron helyét és sebességét egyidejűleg nem határozhatjuk meg tetszőleges pontossággal, így a jövőbeli helyzetét nem tudjuk előre jelezni, tehát az elektron mozgása nem determinált.

Látható, hogy nekünk is sikerült alátámasztani a mikrovilág indeterminizmusáról szóló közfelfogást.  Ez akkor azt jelenti, hogy készen vagyunk, mi sem mondhatunk mást, mint a Wikipédia szócikk írója? A látszat ellenére nincs erről szó, a kapott eredmény ugyanis további vizsgálatra szorul.

A Heisenberg-féle határozatlansági reláció filozófiai interpretációi

 

A kísérlet elemzése során ugyanis rá lehet kérdezni arra, hogy vajon miért nem vagyunk képesek egyidejűleg a pontos hely- és sebesség mérésre? Ezt a kérdést a tapasztalat mögé nézni nem akaró fizikus persze nem teszi fel, ő azt mondja, hogy „a kapott tapasztalat önmagáért beszél, látjuk, hogy az elektron mozgása nem determinált, ezt el kell fogadni.” A jelenségek lehetséges feltételeire is kíváncsi filozófus viszont felteszi ezt a bizonyos kérdést, és a válaszától függően a határozatlansági reláció három különböző filozófiai interpretációját tudja elkülöníteni.

  1. Mondhatjuk azt, hogy azért érvényes az elektron egyidejű hely- és sebesség mérésére vonatkozó Heisenberg-féle korlátozás, mert ilyen a világ, az elektronnak nincs egyszerre pontos sebessége és pontos térbeli helyzete. A kvantummechanika teljesen leírja ezt a világot, de mivel ezekkel az adatokkal az elektron nem rendelkezik egyszerre, az elméleti leírásnak ezt kell visszaadnia. Ezt az értelmezést a határozatlansági relációk ontológiai értelmezésének nevezzük. (Azért fogalmazunk többes számban, mert nem csak a helyre és a sebességre, hanem pl. az energiára és az időre is érvényes) Eszerint a mikrovilágra az indeterminizmus jellemző. (Székely, 74)
  2. De lehetséges az is, hogy bár az elektronnak van pontos helye és sebessége, azokat a kvantummechanika nem képes megragadni, mert a mikrovilágnak nem a teljes leírását nyújtja. Lehetnek olyan, számunkra egyelőre még nem ismert, de megismerhető fizikai jelenségek, ezeket nevezhetjük úgy, hogy „rejtett paraméterek”, amelyeket ha megismernénk, a határozatlansági relációkat ezek felhasználásával levezethetnénk, így a jelenséget determinisztikussá tehetnénk. Ezt a határozatlansági relációk ismeretelméleti értelmezésének nevezzük. Eszerint a fizikai világ determinált, a határozatlanság csak az ismereteinkben lép fel. (Székely, 74)
  3. Egy harmadik lehetőség szerint az elektronnak van ugyan pontos helye és sebessége, de azokat a kvantummechanika nem képes megragadni, mert a számunkra látható és mérhető fizikai jelenségek mögött olyan determinisztikus tényezők húzódnak meg, amelyek számunkra nem megismerhetőek. Eszerint a nézet szerint a kvantummechanika teljesen leírja a mikrovilágot, de a tapasztalt indeterminizmust mégis csak látszólagosnak tekinti, mert úgy gondolja, hogy egy rejtett determinizmus húzódik meg mögötte, amit ugyanakkor az ember nem képes megragadni. Ezt a felfogást a határozatlansági relációk agnosztikus értelmezésének nevezhetjük. (Székely, 74)

A könnyebb megértés kedvéért megpróbálom összefoglalni és újrafogalmazni az előzőeket: a mikrovilág jelenségei az ember számára első közelítésben úgy jelennek meg, mintha ebben a világban az indeterminizmus uralkodna, hiszen nem tudjuk előre jelezni a részecskék jövőbeli helyzetét. De az elemzés egy mélyebb szintje megmutatja, hogy a fizikai leírás nem képes dönteni ebben a kérdésben, a tapasztalt jelenségek három különböző filozófiai interpretációra is lehetőséget adnak. Az egyidejű hely- és sebesség meghatározásban tapasztalt bizonytalanságot értelmezhetjük úgy, hogy:

  1. A kvantumelmélet teljesen leírja a mikrovilágot, de magában ebben a világban van ez a tapasztalt bizonytalanság, a részecskéknek nincs egy időben egyértelmű helyük és sebességük, az „objektíven létező véletlenen” múlik, hogy a jövő egy pillanatában hol fognak tartózkodni. Ezért ezt az értelmezést valószínűségi értelmezésnek nevezzük. Ezt jellemezte úgy Einstein, hogy eszerint „Isten kockázik” és így dönti el, hogy a világ egyes eseményeinek mi legyen a kimenetele. Ez az értelmezés lett az alapja a manapság elterjedt, az egész világ indeterminizmusára vonatkozó nézeteknek.
  2. A kvantumelmélet nem írja le teljesen a mikrovilágot, a leírásból egyelőre hiányoznak bizonyos, előlünk egyelőre rejtett paraméterek, amik felderítése számunkra lehetséges. Ezek felfedezése után a mikrovilágban tapasztalt indeterminizmusról kiderül majd, hogy az csak a kvantummechanika szintjére jellemző. A rejtett paraméterek beépítésével megfogalmazott ún. szubkvantummechanikai szinten az indeterminizmus determinisztikusan megmagyarázhatóvá válik. Ez a rejtett paraméteres értelmezés, erre mondta Einstein, hogy ebben „Isten nem kockázik”, vagyis a természet törvényei nem a valószínűségre épülnek, nem véletlenszerűen dől el, hogy az elektron mikor, hol fog tartózkodni.
  3. A mikrovilág ugyan determinált, de ezt a determináltságot mi soha nem leszünk képesek megérteni, mert olyan szinten dől el, amelyhez az emberi megismerés nem férhet hozzá. A kvantumelmélet teljesen leírja a mikrovilágot a tapasztalati világban, ami számunkra indeterministának látszik. Azonban ez csak egy illúzió, a mélyben valójában meghúzódnak olyan determinisztikus „tényezők”, amelyek meghatározzák ezeket az indeterministának látszó jelenségeket, de ezeket a tényezőket az ember soha nem fogja felfedezni. Ez az agnosztikus felfogás egy öszvér megoldás, az előző két interpretáció egyesítéséből jön létre. Az elsőből átveszi a teljesség, a másodikból pedig a rejtett paraméterek feltevést: a rejtett paraméterek miatt azt mondhatja, hogy a mikrovilág valójában determinisztikus, a teljességi feltevés miatt pedig azt mondhatja, hogy nincs szükség új elméletre, a kvantummechanika helyesen írja le a tapasztalati világot.

A kvantummechanika egyes filozófiai interpretációinak megvalósulásai

 

Az előző fejezetben felsejlett előttünk, hogy a kvantummechanika megértésében az okozza a legfőbb nehézséget, hogy találtak bizonyos matematikai összefüggéseket, amelyeket a mikrovilágra vonatkozó tapasztalataink teljes mértékben alátámasztanak, de ezen matematika értelmezése, ismereteink korábbi rendszerébe való beillesztése fölöttébb kérdéses. Az imént láttuk, hogy filozófiai szinten is lehetséges többféle értelmezés, de a helyzet az, hogy az egyes filozófiai interpretációkon belül is többféle fizikai interpretáció lehetséges attól függően, hogy az egyes matematikai fogalmakhoz milyen konkrét fizikai fogalmakat rendelünk hozzá. Vagyis, van egy működő matematikai rendszer, de nem lehet tudni, hogy mit jelent. Nézzük meg most, hogy az egyes filozófiai értelmezésekhez milyen konkrét fizikai interpretációkat rendelhetünk hozzá.

1.      A valószínűségi értelmezés néhány realizációja

Ezt az értelmezést vallotta Heisenberg, Bohr és az úgynevezett koppenhágai iskola, az ő magyarázataik összességét nevezik koppenhágai értelmezésnek. Mivel ez igen nehezen érthető, sőt néhol ellentmondásos is, több próbálkozás volt a valószínűségi értelmezés szemléletesebb, érthetőbb megfogalmazására, de ezek egyike sem hozott jelentős áttörést a koppenhágaihoz képest.

2.      A rejtett paraméteres értelmezés realizációi

A kvantummechanika kezdeti nagy alakjai közül ezt a nézetet képviselte többek között Einstein, Schrödinger, de Broglie és kicsit később David Bohm. Einstein a kezdetektől fogva ellenezte a koppenhágai iskola valószínűségi értelmezését és több évtizeden keresztül szerette volna bebizonyítani, hogy a kvantumfizika nem adja teljes leírását a mikrovilágnak. Ennek során fogalmazta meg munkatársaival az EPR-paradoxont (Einstein–Podolsky–Rosen-paradoxon). De ennek nem az lett az eredménye, amit Einsteinék vártak, hanem az, hogy a kvantumelméletben megjelent a non-lokalitás jelensége, ami azt jelenti, hogy nagyon távoli események között determinisztikus kapcsolat lehet úgy is, hogy ezt a kapcsolatot semmilyen fénysebességgel terjedő kölcsönhatással nem tudjuk megmagyarázni. (Tehát úgy tűnik, mintha a mikrovilágban lenne olyan „távoli kapcsolat”, amely nem fénysebességgel terjed, hanem úgy, mint a „gondolat”, azonnal megjelenik a világnak egy távoli részén.) Einstein és köre már magát a non-lokalitás jelenségét sem fogadta el, így a rejtett paraméteres interpretációk utáni kutatás ketté vált. Így ma már megkülönböztetjük a lokális és a nem-lokális rejtett paraméteres értelmezéseket.

2.1  Lokális rejtett paraméteres értelmezés

A kvantumelmélet XX. századi művelői között a valószínűségi értelmezés annyira dominánssá vált, hogy egész irodalma van annak a törekvésnek, mely során megpróbálták bebizonyítani a rejtett paraméteres elmélet lehetetlenségét. El is nevezték ezeket „no-go” vagyis „nem-működő” tételeknek. A leghíresebb no-go tétel éppen a magyar származású Neumann Jánoshoz kötődik. Ő 1932-ben közreadott egy bizonyítást arról, hogy nem lehetséges a kvantumelméletnek ilyen értelmezése, és bár ma már elfogadott tény, hogy ez a bizonyítás hibás, de a tétel a XX. század végéig tartotta magát. (A hibára már 1935-ben rámutatott Grete Hermann matematikus, ám érvelésére senki sem figyelt oda, Neumann tételét 1966-ig nem kérdőjelezték meg.). Ekkor John Bell újra rámutatott, hogy a bizonyítás hibás feltevésen alapul, de még mindig évtizedek kellettek, hogy a cáfolat a tudományos közéletben teljes mértékig elfogadott legyen. A tudománytörténet ezt azzal magyarázza, hogy Neumannnak akkora tekintélye volt a XX. század tudományában, hogy a fizika meghatározó alakjai egyszerűen nem hitték el, hogy Ő is tévedhetett! A Neumann-tételhez hasonlóan ma már a többi no-go tételről is kimutatták, hogy jogosulatlan előfeltevéseket tartalmaznak, sőt „Legújabban …a magyar tudományfilozófus, E. Szabó László és neves amerikai kollégája, Arthur Fine közös cikkben mutattak rá arra, hogy lehetséges rejtett paraméteres elméletet alkotni a lokalitás egyidejű megőrzésével.” (Székely, 75) Ezzel a no-go tételek időszaka vélhetően lezárul és újra megnyílt a korábban már lezártnak látszó vita a determinizmus-indeterminizmus kérdéséről.(E. Szabó László, 198)

2.2  Nem-lokális rejtett paraméteres értelmezés

Az imént láttuk, hogy a no-go tételek fékező hatása miatt lokális rejtett paraméteres elméletet eddig még nem sikerült megalkotni és még azt is csak mostanában sikerült bebizonyítani, hogy ez egyáltalán lehetséges. Ezzel szemben David Bohm már 1952-ben megalkotott egy nem-lokális rejtett paraméteres elméletet, ez a Bohm-mechanika, amit viszont nagyon elutasítóan fogadott a tudományos közvélemény, annak ellenére, hogy tökéletesen képes reprodukálni a kvantummechanika minden eredményét. Bohm a valószínűségi értelmezésben feltételezett objektív valószínűségeket egy determinisztikusan viselkedő, az EPR paradoxonnál felvetődött „távoli kapcsolat” véletlen zavaraiként írja le, amivel sikerült episztemológiai korlátozottságként értelmeznie. (Ahhoz hasonló a helyzet, mint amikor egy kockadobás eredményét elvileg pontosan előrejelezhetnénk, ha ismernénk a kockára ható összes testnek és molekulának a helyzetét és sebességét a dobás pillanatában. Ennek a megismerésnek a gyakorlati korlátozottsága okozza a kockadobás során számunkra megnyilvánuló véletlenszerűséget.) „Ahelyett, hogy a Born-féle valószínűségi eloszlásból indultunk volna ki, mint az anyag valamely feltétlen, végleges és megmagyarázhatatlan tulajdonságából, igazoltuk, hogy ez a tulajdonság szubkvantummechanikai szintről eredő véletlenszerű mozgások következménye lehet.” (David Bohm, 163)

3.      Az agnosztikus értelmezés

Ehhez az értelmezéshez nem tartozik önálló fizikai interpretáció, mert ez, mint láttuk, a valószínűségi értelmezés teljes fizikai elméletként történő elfogadásán alapul, így a koppenhágai értelmezés megfelel neki is. De mint önálló filozófiai értelmezés azt bizonyítja, hogy a valószínűségi interpretáció elfogadásából automatikusan nem következik a fizikai világ indeterminizmusa, „a determinizmus-indeterminizmus kérdése még ebben az esetben is megmarad filozófiai kérdésnek.” (Székely, 75)

Összefoglalás

 

Most jutottunk el odáig, hogy válaszolhatunk a Bevezetésben feltett alapkérdésünkre: mikor, hogyan és miért váltotta fel az indeterminizmus a determinizmus dominanciáját a világ jelenségeinek értelmezésében?

Mikor

A szövegben ezt a kérdést már megválaszoltuk. A XX. század elején, a kvantummechanika kialakulásával kezdődött és a valószínűségi értelmezés fősodorrá válásával a század közepére túlnyomórészt lezajlott.

Hogyan

A valószínűségi értelmezés hívei igen hamar a kvantumelmélet fősodrába kerültek. Ebből a pozícióból a maistreamhez nem tartozó elméleteket igen hatékonyan el tudták nyomni. Ezt szolgálták az ún. no-go tételek, amikkel évtizedeken keresztül sikeresen megkérdőjelezték az alternatív interpretációk lehetségességét. De Broglie így számolt be erről az időszakról David Bohm egy 1957-ben kiadott könyvéhez írt előszavában: „1927 májusában egy cikket tettem közzé a Journal de Physique-ben, s itt a hullámmechanika bizonyos kauzális értelmezését vetettem fel. Ezzel a kezdeményezésemmel azonban felhagytam, mert kritikája elbátortalanított. Bohm 1952-ben felelevenítette cikkem néhány gondolatát, … és kifejtve őket, … sikerült fontos érveket találnia a kvantumfizika kauzális értelmezése mellett.” (David Bohm, 5) Tehát még olyan, már neves tudóst is el tudtak bizonytalanítani, mint de Broglie, hát akkor a fiatal tehetségek hogy mertek volna velük szembe menni? De ha szükség volt rá, a fizikán kívüli érveket sem vetették meg, sőt használják a mai napig: „Ami a Bohm-féle interpretációt és annak különböző változatait illeti, vele szemben még a koppenhágai interpretáció legelkötelezettebb hívei is csupán metateoretikus érvet tudnak felhozni: arra hivatkoznak, hogy a távolba hatás megengedése túl nagy ár a determinizmus megmentése érdekében, mivel metafizikai elemet épít be a fizikába, és sérti az Ockham-borotva elvét.” (Székely, 76)

Miért

Miért a valószínűségi értelmezés hívei kerültek a fizika tudományának a fősodrába? Azért, mert ez a filozófiai interpretáció illeszkedett legjobban a filozófia XX. századi materialista, pozitivista, metafizika ellenes fősodrába. És megfordítva is igaz, a filozófiai fősodor ettől a kvantummechanikai interpretációtól várhatta leginkább a maga további megerősítését.

A valószínűségi interpretáció, a korábban csak episztemikusan értelmezett véletlenszerűség helyett bevezette az ontológiai véletlenszerűség fogalmát.

A véletlenszerűség episztemikus értelmezése szerint a véletlenség csak az oksági magyarázat "hibája". A determinizmus modern felfogásában abból indulunk ki, hogy mivel "miden összefügg mindennel", minden egyes jelenséget egy végtelen sok tényezőből álló oksági rendszer határoz meg, de egy konkrét oksági magyarázatban ebből a számtalan tényezőből mindig csak véges sokat vehetünk figyelembe. Viszont azon oksági tényezők, amelyeket az adott leírásban elhanyagolunk, valamilyen mértékben természetesen szintén befolyásolják az adott jelenséget, így az oksági magyarázatunk soha nem lehet teljes. De ha jól választottuk ki a magyarázatba bevont okokat, akkor az elhanyagolt tényezők csak olyan kis mértékben lesznek felelősek a jelenség kimeneteléért, hogy ezeket már összevonva a leírás véletlen hibájaként foghatjuk fel. Kis módosítással érvényes ez a felfogás az olyan típusú jelenségekre is, mint a kockadobás. Ebben az esetben nem tudunk kiragadni néhány domináns tényezőt a végtelen oksági rendszerből, ezért az összes lehetséges okot összevonjuk, és úgy kezeljük, hogy az adott jelenséget csak véletlen tényezők hatásaként tudjuk leírni, de elvileg rájuk tudunk mutatni, csak olyan sokan vannak, hogy az ember nem képes őket számba venni. A véletlenszerűség ontológiai felfogása szerint viszont a mikrovilágban tapasztalt véletlen jelenségeknek elvileg sincsenek okai, azok ontológiailag nem meghatározottak. Tehát nem arról van szó mint a kocka esetében, ahol tudjuk, hogy az eredmény az eldobáskor a kockára ható forgatónyomatéktól, az asztal felületétől, a levegő számtalan részecskéjétől stb. függ, amiket elvileg figyelembe tudnánk venni. Ebben az esetben úgy fogjuk fel, hogy ilyen oksági tényezők nincsenek, ezért a mikrovilág jelenségei tisztán véletlenszerűen alakulnak.

A véletlenség ezen ontológiai felfogása remek lehetőséget nyújtott a materialista filozófiának arra, hogy a tapasztalati világ transzcendens előfeltételét valló idealista világnézet metafizikai entitását (Istent) közvetlenül lecserélje erre a kvantummechanika által fizikai entitásként értelmezett véletlenszerűségre, és ezzel megalkossa a materialisták mindenhatóját, a „Véletlent”. Ez persze szükségképpen metafizikai fogalom maradt, hiszen egy filozófiai interpretáció választás eredményeként született, így a kvantummechanika sem bizonyíthatta be róla, hogy az anyagi világ objektív megnyilvánulása lenne. De nagyon jól tudják használni a metafizikai vonatkozású kérdések megválaszolásakor, mert eredete miatt megmaradt a metafizikai magyarázó ereje, ugyanakkor a hozzá kapcsolódó filozófiai választást sikerült annyira elrejteni, hogy el tudják hitetni, előbb a fizikus szakma legtöbb képviselőjével, az ő segítségükkel pedig a szélesebb közvéleménnyel is, hogy a véletlen az anyagi világ része. Így a fizikai világ jelenségeinek magyarázatához használva azt a látszatot tudják kelteni, hogy benne maradnak az anyagi világban, ők nem folyamodnak tapasztalatilag nem megragadható metafizikai entitásokhoz, pedig a fenti érvek szerint ők maguk is egy metafizikai fogalmat használnak.

(Érdemes itt megjegyezni, hogy a materialisták egy másik, hasonló csúsztatást megengedő fogalma a végtelen. Ez is rendelkezik metafizikai magyarázó erővel, hiszen megvan a metafizikai gyökere, ugyanakkor matematikai fogalomként objektív és az anyagi világ részét képező entitásként is meg lehet jeleníteni. Ezért lehet olyan sikeresen a végtelen tér és idő fogalmának a felhasználásával érvelni az anyagi világot valamilyen transzcendens entitásból eredeztető idealista világnézet ellen, de ez már egy másik bejegyzés témája.)

Összefoglalva: a kvantummechanika és az indeterminizmus egymáshoz való viszonya pont fordítottja annak, mint amit manapság a közvélemény gondol róla. A helyzet úgy áll, hogy a kvantummechanika valójában nem bizonyította be, hogy a világ működése indeterminisztikus lenne, hanem az elmélet néhány domináns megalkotója egyénileg is különböző filozófiai megfontolásokból vélték úgy, hogy a világ nem determinisztikusan működik, és ennek lett a következménye a kvantummechanika indeterminisztikus értelmezése. (Vö: Székely, 80)

 

Irodalom

 

 

 

Kiegészítés: 2016. augusztus 31.

  • A Heisenberg-féle határozatlansági reláció filozófiai interpretációit ki kell még egészíteni az úgynevezett statisztikai értelmezéssel. Ez a felfogás, az agnosztikus értelmezéshez hasonlóan a valószínűségi felfogás és a rejtett paraméteres értelmezés egyesítéséből jön létre. A tények alapján ez az interpretáció is elfogadja, hogy a mikrovilág eseményei valószínűségi jellegűek, de úgy fogja fel, hogy a határozatlansági reláció csak egy statisztikai összefüggés, annak csak nagyszámú, azonos rendszeren elvégzett kísérlet esetén van jelentése, egy egyedi eseményre nem vonatkoztatható. Az egyedi eseményeket a feltételezett rejtett paraméterek determinisztikusan meghatározzák, de ezt ahhoz hasonlóan teszik, mint ahogy a kockadobás eredményét meghatározza a számtalan determinisztikus mechanikai tényező. Ebben az esetben a nagyszámú, azonos rendszeren elvégzett kísérletben kapott hely vagy sebesség értékek szórása fog megegyezni a határozatlansági reláció által jelzett bizonytalansággal. Ez az értelmezés tehát nem fogadja el sem azt, hogy a kvantummechanika a mikrofizikai valóság teljes leírását adná, sem azt, hogy a leírás az egyedi rendszerekre vonatkozna. A rejtett paraméterek feltevéssel élve elveti az indeterminizmust, közben az episztemológiai véletlennel értelmezi az események valószínűségi jellegét. Ez az értelmezés a koppenhágai értelmezésben megfogalmazott paradoxonokat könnyen meg tudja magyarázni. Például a koppenhágai értelmezés abszurditását bemutató „Schrödinger macskája” kísérlet itt nem paradoxon, hiszen a statisztikai értelmezés miatt a radioaktív mag elbomlására adott valószínűség azt jelenti, hogy a kísérletek egy részében a mag elbomlik, így a macska meghal, egy részében meg nem bomlik el, így a macska tovább él.
  • Az alábbi táblázatban át tudjuk tekinteni az egyes filozófiai interpretációkat a legfontosabb szempontok szerint.

 

név1

név2

egyedi leírás

filozófia

teljesség

rejtett paraméter

rejtett paraméter megismerhető
1

ontológiai

valószínűségi

egyedi

indeter-minista

teljes

nincs

-

2

ismeret-elméleti

rejtett paraméteres

egyedi

deter-minista

nem teljes

van

igen

3

agnosztikus

 

egyedi

deter-minista

teljes

van

nem

4

statisztikus

 

sokaság

deter-minista

nem teljes

van

igen
  • Végül szólnom kell az egyes interpretációkra vonatkozó szóhasználatról is, ez ugyanis a kvantummechanikával foglalkozó szakirodalomban nem egységes.
    • A táblázatban szereplő 1. számú ontológiai értelmezés a régebbi szakirodalomban néha statisztikusként van említve, de ez nem azonos az általam a 4. pontban leírt statisztikus értelmezéssel.
    • A név2-ben használt elnevezéseket saját használatra vezettem be, mert elég találónak tartottam, de néha ütközik a szakirodalom szóhasználatával: például a 4. számú statisztikust néha valószínűségiként is említik.
    • A 2. számú rejtett paraméteres elnevezésben van egy kis ellentmondás, hiszen a 3. és 4. számú is rejtett paraméteres. A táblázat remélem feloldja ezt az ellentmondást.
19 komment
Címkék: véletlen fizika szabad akarat kvantummechanika agnosztikus kvantumfizika mainstream okság determinizmus kvantumelmélet Fizika fősodor főáram melléksodor Cs. Horváth János indeterminizmus rejtett paraméterek Bohm Bohm mechanika Csebó Horváth János

Ajánlott bejegyzések:

A bejegyzés trackback címe:

https://melleksodor.blog.hu/api/trackback/id/tr228905752

Kommentek:

A hozzászólások a vonatkozó jogszabályok  értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai  üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a  Felhasználási feltételekben és az adatvédelmi tájékoztatóban.

Birgi Zorgony 2016.08.05. 12:02:04

Az világos volt a bejegyzésből, hogy nem a kvantummechanika támasztotta alá az indeterminizmust, hanem néhány tudós „indeterminisztikus prekoncepciója” vezetett el a kvantummechanika koppenhágai értelmezéséhez. Valószínűleg nem ez az egyetlen olyan eset, amikor tudományon kívüli tényezők határozzák meg a tudományos nézeteket. Az azonban nem volt világos – legalábbis számomra –, hogy miért kapcsolódna erősebben az indeterminizmus a materializmushoz, mint a determinizmus.

Először is a koppenhágai értelmezés egyik legkiválóbb képviselője, Heisenberg kifejezetten nyitott volt a világ nem-materialisztikus értelmezésére. Igaz, a másik oldalon is volt ilyen (Schrödinger).

Másodszor a determinisztikus értelmezés a XIX. századhoz kapcsolódott. Viszont e század kifejezetten a tudomány materialisztikus értelmezésének és önhitt mindentudásának százada volt. Míg a determinizmus a mechanisztikus felfogáshoz kapcsolódik inkább, az indeterminizmus a világ egy szubtilisabb értelmezéséhez.

Harmadszor a kvantummechanika indeterminisztikus értelmezésére tudtommal sokszor és sokan tekintettek úgy, mint a biológiai életben és a tudatos létben megnyilvánuló indeterminizmus fizikai alapjára, hiszen a szigorú determinizmus világában nincs helye a szellem szabadságának (vö. „szabad akarat”).

Mindebből számomra az következik, hogy a XX. századi természettudományos mainstream elkötelezettségét a kvantummechanika indeterminisztikus interpretációja mellett más tényezők határozhatták meg, mint amit te említesz a bejegyzésedben.

Továbbá ha egyszer az általad megfogalmazott kérdést nem lehet eldönteni szigorúan tudományos alapon, vagyis ha a kvantummechanika mint olyan nem gondoskodik saját értelmezéséről, akkor a kvantummechanikához képest külső szempontokat kell figyelembe venni. Ha viszont külső szempontok fognak dönteni a kvantummechanika determinisztikus vagy indeterminisztikus értelmezésének kérdésében, akkor a kvantummechanikát el is lehet hagyni, és érdemes csupán „tisztán” a „külső” szempontokra irányítani a figyelmet, mert ezek összevetése – kvantummechanikai referencialitásuktól függetlenül – sokkal nagyobb eredménnyel kecsegtet, mint összekapcsolódva egy bonyolult fizikai jelenséghalmazzal. Magyarán a probléma nem természettudományos, vagyis a kvantummechanika szóban forgó értelmezésének kulcsa nem a kvantummechanikában található. Ez az értelmezés már csak azért sem lehet kvantummechanikai, mert bármi mellett is döntsünk, maga a megoldás is jóval túlmutat a természettudomány kompetenciáján. Nem lehet ugyanis pusztán természettudományos alapon megoldani olyan kérdéseket, amelyeknek megoldása túlmutat a természettudományok határain. Ez talán tautologikusnak látszik, de egyáltalán nem az, hanem szerintem egy lényeges hermeneutikai alapelv.

Ha pusztán szakmai – természettudományi – kérdésről lenne szó, természetesen akár Bohr, akár Heisenberg, akár Schrödinger, akár Einstein álláspontját felülbírálni enyhén szólva merész dolog volna egy olyan ember számára, akiknek tudása e tekintetben még elhanyagolhatónak is csak nagy jóindulattal tekinthető az említett urakéhoz képest. (Ezúttal természetesen magamról beszélek.) Ellenben ha a tökéletesen kompetens fizikusok nem értenek egyet egymással egy világszemléleti horderejű kérdésben, akkor ebből nagy valószínűséggel az látszik, hogy a kérdés gyökerei nem természettudományos jellegűek.

Emiatt – és egyébként az általad megfogalmazott fordított kauzalitásnak megfelelően (a tudósok filozófiai háttérszemlélete határozta meg kvantummechanika-értelmezésüket) – úgy gondolom, hogy mindenekelőtt a véletlen és a determinizmus fogalmát kellene tisztázni ahhoz, hogy a kettő egymáshoz való viszonya átlátható legyen, s hogy a kvantummechanika értelmezésének kérdésében laikusként is állást foglalhasson az ember. Ugyanis nem a kvantummechanika fogja eldönteni, hogy a világ determinisztikus vagy indeterminisztikus, hanem a kettő közötti választás fogja eldönteni, hogy a kvantummechanikát hogyan kell értelmezni. Nem lenne jó ugyanis elkövetni azt a hibát, amit a determinisztikus és az indeterminisztikus értelmezés képviselői egyaránt elkövettek, hogy tudniillik saját filozófiai hátterük nyílt tisztázása nélkül fogtak neki egy tudományos tényanyag rejtetten filozófiai értelmezésének.
Válasz erre 

Csebó Horváth János 2016.08.09. 16:43:54

Köszönöm a kommentet, az alábbiakban megpróbálok röviden válaszolni a felvetett kérdésekre, de ehhez néhány ponton ki kell lépnem az eredeti szöveg keretei közül.

1. Nézzük először a determinizmus fogalmát. Szerintem az „élettelen világra” érvényes az oksági determinizmus elve, vagyis az, hogy „az élettelen világ állapota egy bizonyos időpontban együtt a természeti törvényekkel meghatározza a világ későbbi állapotait”. Hangsúlyozom, hogy ezt az elvet csak az élettelen világra tartom igaznak, mivel szerintem az élettelen és az élő világ között létezik egy ontológiai szakadék, ami miatt az élettelen világra érvényes természettörvények nem írják le az élő világot a maga teljességében. Ezen a szinten ugyanis léteznek olyan specifikus, csak az életre jellemző „mozgástörvények”, amikről még nem sokat tudunk, és úgy vélem, hogy a létezés három nagy ontológiai szintje (élettelen, élő, ember) között a természettudomány nem találja az átjárást, ugyanis az evolúció vagy az emergencia fogalma a „szintek közötti létra” funkciót nem tudja betölteni.

2. Azzal, hogy az élő világot (részben) kiemeljük az élettelen világra érvényes törvények hatálya alól, egyszerre biztosíthatjuk a determinizmus elvét és a „szabad akarat” lehetőségét. Ha a determinizmus elvét csak az élettelen világra vonatkoztatjuk, a szabad akarat elvét pedig csak az élőre, a két elv antagonisztikus ellentéte feloldódik. A két elv együttes alkalmazásával az ember megmentheti hagyományos világszemléletét: a determinizmus elvére alapozhatja a világ kiszámíthatóságában, míg a szabad akarat elvére a saját szabadságában való hitét. Ugyanakkor a „szabad” élő szféra a determinista élettelen szintre lehet olyan hatással, hogy a determinizmusból következő fatalizmus szóba sem jöhet.

3. „Miért kapcsolódna erősebben az indeterminizmus a materializmushoz, mint a determinizmus”?

-A szövegben azzal érveltem, hogy a materialista főáram azért karolta fel a kvantummechanika valószínűségi értelmezését, mert remek lehetőséget látott a maga számára az itt megfogalmazott ontológiai véletlen fogalmában. És bár a véletlen fogalmát már korábban is használták a materialista világértelmezés kifejtésekor, ez a korábbi véletlen fogalom csak az ismeretelméleti felfogáson alapult, így a rá épített magyarázatok könnyen támadhatók voltak. Azzal azonban, hogy a kvantummechanika valószínűségi értelmezésével kapott véletlen fogalmat „megkérdőjelezhetetlen, a tudomány által felfedezett objektív anyagi jelenségként” lehet felmutatni, a fogalomnak a világnézeti érvelésben elfoglalt súlya egy nagyságrenddel megnőtt.

- Az valószínű, hogy Heisenberg és Bohr nem volt materialista, Székely szerint Heisenbergre Fichte, Bohr-ra Kierkegaard idealista filozófiája volt hatással. (Bohr emellett, paradox módon erősen pozitivista is volt.) Nyilván felhasználható az indeterminizmus nem materialista nézetek alátámasztására is, de azt gondolom, erre a célra manapság már kevésbé hatékony. A szabad akaratnak a határozatlansági elvből való eredeztetése például egyenesen megmosolyogtató. De az „objektív véletlen, mint az anyagi világ mindenható teremtője”, nagy lehetőséget ad a materialista szemlélet számára.

- Az igaz, hogy a XIX. századi materialista világnézet a determinizmus akkori változatára, a mechanisztikus determinizmusra támaszkodott, és az is igaz lehet, hogy most is összhangba hozható a determinizmus és a materializmus, de én úgy látom, hogy a materialista főáram most inkább az indeterminizmust preferálja és az objektív véletlen fogalmát használja minden lényeges világnézeti kérdésben az anyag keletkezésétől kezdve az élet kialakulásán át a tudat létrejöttéig.

4. Meglehet, hogy „a XX. századi természettudományos mainstream elkötelezettségét a kvantummechanika indeterminisztikus interpretációja mellett más tényezők határozhatták meg,” mint amit én megjelöltem a bejegyzésben, de mivel abban biztosak lehetünk, hogy nem „az objektív véletlen műve” :) volt ez az elkötelezettség, kíváncsi lennék rá, hogy milyen egyéb tényezőkre gondolsz?
Válasz erre 

Birgi Zorgony 2016.08.10. 12:20:06

Az indeterminizmus értékelésében egyetértek veled, de kissé másképpen közelíteném meg a megoldást. Ahogy az előző kommentben is utaltam rá, a kvantummechanika értelmezésének nagy problémáját érdemesebb a kvantummechanikától függetlenül, magának a problémának (determinizmus kontra indeterminizmus) a szintjén vizsgálni.

Az indeterminizmus véleményem szerint eufemisztikus megfogalmazás, akárcsak a „véletlenszerűség”. Ha ezeket nevükön nevezzük, máris látszik valami abból a problémahalmazból, amelyet ezek a megfogalmazások elrejteni igyekeznek. Ha bejegyzésed elején említett négy pontot ennek megfelelően átfogalmazom, akkor nagyon jól érzékelhető az elmélet – hogy finoman fogalmazzak – intellektuálisan lehangoló színvonala:

1. a világ véletlenül keletkezett a semmiből;
2. az Univerzum jelenleg megfigyelhető struktúrája véletlenül alakult ki az anyag egy alacsonyan strukturált állapotából;
3. az élő organizmusok véletlenül jöttek létre az élettelen anyagból;
4. az öntudattal bíró ember véletlenül fejlődött ki a primitív élő organizmusokból.

Ugyanerre az eredményre juthatunk, ha a „indeterminizmus” szót felcseréljük arra, amit tulajdonképpen elfed és maga mögött rejt: a-kauzalitás, vagyis oknélküliség. A kvantummechanika indeterminisztikus értelmezése ugyanis azt mondja ki, hogy vannak olyan okozatok, amelyeknek nincs oka; vannak történések, amelyek ok nélkül mennek végbe; vannak következmények, amelyeknek nincs előzménye. Ez nemcsak az általános megmaradási elveknek, illetve ezek tudományosan kevésbé ismert komplementerének mond ellent (tömeg/energia/impulzus nem keletkezik a semmiből), hanem ezek filozófiai alapjának is: a lét „mennyiségét” a léten belül sem növelni, sem csökkenteni nem lehet – ez ugyanis isteni privilégium (creatio ex nihilo / reductio ad nihilum). Ha ugyanis nem így lenne, akkor egy teremtői funkció átkerülne a teremtményhez.

Egyébként is nagyon furcsa lenne, hogy ha a világon belül, melynek működését minden ízében törvények szabályozzák, volna egy olyan terület, amely semmiféle törvényszerűségnek nincs alávetve, amikor még véletlengenerátorral is csak álvéletleneket lehet előállítani. Ha volna véletlen a szó tudományos – indeterminisztikus – értelmében, akkor az valamiképpen nem lenne része ennek a világnak. Miközben mindent törvények szabályoznak, ez az egy kívül állna minden törvényszerűségen. Illetve csak félig: ugyanis félig-meddig kívül állna minden törvényszerűségen, félig-meddig viszont maga is alá lenne vetve véletlen „megmozdulása” után bizonyos törvényeknek. Abszurd feltételezés, hogy világunkon belül lehetne valami, aminek nincs oka, de amely okként szerepel, illetve egy ideig nincs alávetve törvényeknek, majd érvényesek lesznek rá is a törvények. Efféle „objektív véletlen” létét a modern tudományosság előtti filozófia soha nem feltételezte, mert kimondatlanul is tisztában volt azzal, hogy egy objektív véletlen objektív nonszensz.

A klasszikus értelemben vett véletlen tulajdonképpeni értelmét magának a szónak az etimológiája mutatja: „nem vélt”, „előre nem látott”, „váratlan”. Mindaz, amit a fizika „véletlenszerűnek” tekint, voltaképpen a szó eredeti értelmében vett vél-etlen. Így például az instabil radioaktív izotópok atomjainak átalakulása stabil izotópokká is csak annyiban „véletlenszerű”, amennyiben (hogy a makrovilágban keressünk analógiát) a sörhab buborékainak elpattanása is „véletlenszerűen” történik. Ez esetben sem lehet ugyanis megmondani, hogy éppen melyik buborék fog elpattanni, noha többé-kevésbé világosan meg lehet határozni az instabil sörbuborékok stabil „söratomokká” való átalakulásának menetét, és például a Kőbányai Világos habjának és a Dreher Bak habjának felezési ideje között szignifikáns a különbség, miközben az összes habbuborék elpattanása – akárcsak a radioaktív izotópok esetében – ezúttal is indifferens.

Véleményem szerint az indeterminisztikusnak tekintett fizikai-kémiai folyamatoknak éppen a statisztikai determináltsága mutatja, hogy az egyedi esetekben is jelen kell lennie valamilyen determináltságnak, mert nem lehet, hogy egyedileg teljességgel meghatározatlan történések nagyon is meghatározott, vagyis törvényeknek alávetett statisztikai képet mutassanak. A fa ágai is „véletlenszerűen” ágaznak-bogaznak, mégis szigorú rend szerint alkalmazkodnak a korona habitusához. Mindaddig, amíg a tudomány nem fedezi fel az „egyedi” és „közös” közötti – nyilvánvalóan jelenlévő és ható – törvényszerűséget, illetve e törvényszerűség „működési mechanizmusát”, még véletlenül sem jelentheti ki az „egyedi” véletlenszerűségét. Ha viszont e „közvetítő” törvényszerűséget megtalálta, nagy lépést tett az „egyedire” vonatkozó törvények felismerése felé is.
Válasz erre 

Birgi Zorgony 2016.08.10. 12:21:16

A másik kérdés az indeterminizmus modernkori tudományos megjelenésének oka. A te értelmezésedet az említett megszorításokkal akár elfogadhatónak is tartom, de jómagam mégis másként közelíteném meg a kérdést. Bevallom, e tekintetben csak tapogatózni tudok, de azért megkísérelem felvázolni, hogy milyen okokat sejtek e változás mögött.

A premodern (természet)filozófiák mindig is „deterministák” voltak, de erős teleologikus felhanggal – vagyis úgy vélekedtek, hogy mindennek megvan a maga oka, és ok, illetve cél nélkül semmi sem történik. Ezzel együtt a természet világán belüli ok-okozati összefüggés csak kevéssé tartozott érdeklődési körükbe. Érdeklődésük homlokterében más állt. A XIX. századra a természettudományok természettudományos törvényekkel hálózták be a világot, s e kort annak eufórikus tudata hatotta át, hogy mindent törvények szabályoznak, ezeket a törvényeket pedig meg lehet ismerni. Ezért lehet a XIX. századot a determinizmus klasszikus időszakának tekinteni. A XX. század sok mindent örökölt a megelőző századoktól, és sok minden továbbél még ma is, de azért jelentős változások is végbementek. A modernség új korszakába lépett. A szigorú természettörvények által irányított mechanisztikus világ képe már nem vonzotta a XX. századi embert. Ami a kort filozófiailag legmélyebbről jellemzi, az az ember felszabadításának vágya mindennemű represszív hatalom alól. A posztmodernizmus természettudomány-ellenessége mögött is az rejlik, hogy minden objektivitás korlátot szab a szubjektumnak és a szubjektivitásnak, s ezáltal elnyomja. Véleményem szerint az indeterminizmus megjelenése ebbe a folyamatba illeszkedik, és a törvényeknek való alávetettség helyett a törvényektől való szabadság irányába való elmozdulást képviseli. Vagyis a XIX. század mechanisztikus determinizmusa és a XX-XXI. század „dialektikus indeterminizmusa” (hogy ilyen marxista ízű ellentétpárral éljek) nem ellentétben áll egymással, hanem ugyanazon tudományfilozófia, ugyanazon tudományos fejlődés két, egymás után következő fázisát képviseli.

Ennek ellenére – és immár pusztán az elvek síkját nézve – természetesen nem gondolom, hogy ez az elmozdulás a valódi szabadság irányába mutatna. Akár a véletlen(szerűség)et, akár az indeterminizmust nézzük, az a determinációtól és a törvények által fenntartott rendből való kiszabadulás torz formája, egy olyan ad absurdum vitt öntörvényűség, amely már átfordult öntörvénytelenségbe. Az indeterminizmus pervertált és üres szabadság, mert a tartalma tiszta negativitás: senki és semmi ne határozzon meg. A „véletlen(szerűség)” pedig leleplezi ennek a „szabadságnak” a működési mechanizmusát és tartalmát. A szabadság lényege ugyanis nem az akauzalitás, hanem az autonóm teleologikusság: a szabadon megválasztott célirányosság.
Válasz erre 

Csebó Horváth János 2016.08.15. 00:59:36

- Megjegyzéseiddel lényegében egyet értek, bár néha hiányzik egy-egy bevezető gondolatsor a saját filozófiai pozíciód kifejtésénél. Az általad alkalmazott „in medias res” érvelési módszer nem nagyon segíti az olvasót abban, hogy a sokszor elég szokatlan nézeteidet legalább részben megértse. Ezt éreztem például a következő, az ontológiai véletlen fogalmához fűzött megjegyzésedben: „a lét „mennyiségét” a léten belül sem növelni, sem csökkenteni nem lehet – ez ugyanis isteni privilégium”. Mivel manapság nem sokan foglalkozhatnak Aquinói Szent Tamás és a skolasztikusok ontológiájával, néhány szóval jó lett volna bevezetni ezt a különben igen magvas gondolatot, és közben rámutatni arra a filozófiai álláspontra, amiből ez született.

- Zorgony írta: „Véleményem szerint az indeterminisztikusnak tekintett fizikai-kémiai folyamatoknak éppen a statisztikai determináltsága mutatja, hogy az egyedi esetekben is jelen kell lennie valamilyen determináltságnak, mert nem lehet, hogy egyedileg teljességgel meghatározatlan történések nagyon is meghatározott, vagyis törvényeknek alávetett statisztikai képet mutassanak.”
Bármilyen ésszerű amit itt írsz, ez a koppenhágaiakat nem győzte meg. (Einstein nagyon hasonlóan érvelt az egyik írásában: Albert Einstein válogatott írásai, Typotex 2005, 219.o.) Bohrék ahelyett, hogy elfogadták volna az egyedi rendszer kínálkozó rejtett meghatározottságát, inkább azt a megoldást választották, hogy elvetették az egyedi esemény fogalmát: szerintük az az esemény, hogy egy atom kibocsát egy α-részecskét nem is létezik, mert erről csak akkor tudnánk meggyőződni, ha egy mérést végeznénk, de a mérés eredményéből nem lehetne arra következtetni, hogy mi lett volna, ha a mérést nem hajtjuk végre. Az egyedi esemény ezen indeterminista felfogása az alapja a „Schrödinger macskájaként” elhíresült problémafelvetésnek, melyben Schrödinger azt mutatja be, hogy ha az egyedi kvantummechanikai esemény létezését az indeterministákkal egyetértve elvetjük, az azt eredményezi, hogy egy ilyen eseménytől függő dobozba zárt macska félig élő és félig holt lesz mindaddig, amíg meg nem mérjük, hogy a dobozban lévő atommag elbomlott-e, vagy nem. Mivel Schrödinger szerint ez magának a makro fizikai valóságnak a teljes megcsúfolása, ezért az egyedi esemény létezését nem vethetjük el, de akkor fel kell tételeznünk azok rejtett meghatározottságát.
A probléma indeterminista értelmezéséről a Wikipédiában most ezt olvashatjuk:
„A kísérletnek legalább három eltérő értelmezése létezik.
1. Feltételezhetjük Isten létezését. Mivel minden megfigyeléshez kell egy megfigyelő, kell lennie valamilyen „tudatosságnak” az Univerzumban. Wigner Jenő fizikus úgy gondolta, hogy maga a kvantumelmélet egyenesen bizonyíték Isten létére.
2. A legtöbb gyakorló fizikus nem vesz tudomást róla. Néhányuk rámutat, hogy egy kamera mindenféle tudatosság nélkül rögzítheti a macska állapotát.
3. A sokvilág-elmélet szerint minden kvantumvilág létezik és ezek útelágazáshoz hasonlóan kapcsolódnak egymáshoz. Az egyik ilyen világban a hidrogén-cianidos üveg összetört és a macska meghalt, míg egy másikban ez nem történt meg és a macska életben maradt.”
(Vö: hu.wikipedia.org/wiki/Schr%C3%B6dinger_macsk%C3%A1ja)
Látható, hogy az indeterministák a mai napig nem tudtak meggyőző választ adni erre a problémára, így könnyen lehet, hogy ez lesz az a pont, ahol be kell adják a derekukat és fel kell adják az egyedi mikrofizikai eseményt tagadó álláspontjukat, és ezzel a együtt a kvantummechanika valószínűségi értelmezését.
(Most látom csak, hogy az indeterministák Wigner Jenő féle szubjektív idealista felfogását eddig teljesen figyelmen kívül hagytam, amit már én is hiányolok. Egy későbbi bejegyzésben megpróbálom pótolni ezt a hiányosságot.)

- Zorgony írta: „Ami a kort filozófiailag legmélyebbről jellemzi, az az ember felszabadításának vágya mindennemű represszív hatalom alól.”
Köszönöm a kiegészítést, ami természetesen finomítja az én kissé leegyszerűsített magyarázatomat, de úgy gondolom, alapvetően nem mond annak ellent, a két magyarázat összhangba hozható.
Válasz erre 

Birgi Zorgony 2016.08.16. 20:53:32

1. A megmaradási törvények egy olyan filozófiai evidencia tudományos igazolását adják, amely már jóval a modern természettudomány megjelenése előtt is ismert volt, és amelyet a legegyszerűbben talán így lehetne megfogalmazni: az ember éppúgy nem képes teremteni – az isteni creatio ex nihilo értelmében –, mint ahogy ennek reciprokaként megsemmisíteni sem képes. Létet semmiből létrehozni, illetve létet semmivé tenni: e kettő egyazon „képesség” két oldala. Az ember számára nincs „átjárhatóság” a semmi és a lét között, ugyanis maga is a lét világába tartozik. E filozófiai álláspont szerint Isten számára azért van lehetőség teremteni és megsemmisíteni, vagyis azért állhat fölötte mind a létnek, mind a nemlétnek, mert birtokában van a lét és a nemlét közös gyökerének.

A modern természettudomány ennek a filozófiai axiómának a természettudományos specifikációit fogalmazta meg a megmaradási törvényekben. Filozófia és természettudomány itt tehát egyazon igazság két ellentétes oldalát ragadta meg. Míg ugyanis a filozófiát elsősorban a semmi→lét irány érdekelte (semmiből való teremtés), addig a természettudományt a lét→semmi irány érdekli (tömeg/energia/impulzus egy zárt rendszeren belül nem veszhet el, vagyis nem semmisülhet meg).

Bár nem tudok arról, hogy volna kauzalitás-megmaradási törvény, de úgy gondolom, hogy az energia-megmaradás csupán egy másik megnevezése ennek, tekintve, hogy az oksági kapcsolat egyúttal energia-viszony is. Ha pedig ez így van, akkor az indeterminizmus sérti az energia-megmaradás elvét, mert ok nélküli okozatot tételez. Ezért szerintem a kvantummechanika indeterminisztikus értelmezését mind filozófiai, mind természettudományos alapon el kell vetni.

2. Ha felszámoljuk az egyedi esemény fogalmát, vagyis magát az egyediséget, akkor voltaképpen felszámoljuk a determinizmus/indeterminizmus problematikát is. Ha ugyanis nincs egyedi esemény, akkor nincs determinizmus, de indeterminizmus sincs, mert e fogalomnak megszűnik a fix vonatkoztatási pontja. Talán paradoxnak hangzik, de az indeterminizmust csak valami determinált, meghatározott vonatkozásában mondhatjuk ki, mert az indeterminált a determináltságból kilépve lesz indeterminált, mint ahogy a csoda is a természet törvényeinek áthágása által lesz csoda. Másfelől azonban az egyediség felszámolása már önmagában véve is indeterminizmus, csak éppen nem kauzális, hanem – mondhatni – ontológiai indeterminizmus: egy „dolognak” vagy „folyamatnak” nincsen körülhatárolható azonossága, hanem egyfajta „ontológiai elmosódottsággal” bír. Ezt az „ontológiai elmosódottságot” nevezi a kvantummechanika valószínűségnek.

Ha viszont így van, akkor tulajdonképpen már magunk mögött is hagyhatjuk a determinizmus/indeterminizmust problematikát, hogy egy – érzésem szerint – alapvetőbb problémával szembesüljünk: kvantummechanikai szinten semmi sem az, ami. Egy ilyen kijelentés talán botrányosnak tűnhet (mint ahogy a kvantummechanika determinisztikus értelmezői számára annak is tűnt), de szerintem nem feltétlenül az. Ez a kijelentés ugyanis nemcsak a kvantummechanikai eseményekre igaz. Arra gondolok, hogy ha kétszer nem lehet ugyanabba a folyóba lépni, akkor ez azt jelenti, hogy annak a folyónak nincsen megragadható – időben megragadható – önazonossága. A gondolat első megfogalmazója Nyugaton tudvalevőleg Hérakleitosz volt. Egyik viszonylag kései követője, Kratülosz azonban egészen odáig ment, hogy kijelentette: már egyszer sem lehet ugyanabba a folyóba lépni. Ez azt jelenti, hogy a folyónak nemcsak időben megragadható önazonossága nem létezik, hanem pillanatnyi önazonossága sem. A távol-keleti bölcselet pedig egyenesen az állítja, hogy nem lehet valóságos az, ami a permanens identitásvesztés állapotában van, vagyis ami – à la Kratülosz – egyetlen pillanatban sem rendelkezik önazonossággal; illetve ami valóságos, az nem másulhat meg folytonosan. És pontosan ez a nem valóságosság az „ontológiai elmosódottság”.

Hérakleitosz és Kratülosz természetesen csak a „gyengébbek kedvéért” beszélt folyóról: voltaképpen semminek, egyetlen entitásnak és egyetlen folyamatnak sincsen önazonossága. Vagyis nem arról van szó, hogy „vagy valami, vagy megy valahová” (mint ahogy a székely vicc mondja), hanem arról, hogy ami valami, az is megy valahová, és éppen ez a „valahová menés” az, ami mindennek az ontológiai elmosódottságát adja. Egy folyó tehát éppúgy csak „statisztikailag” ragadható meg, mint ahogy egy α-részecske kibocsátása is.

Ha tehát a kvantummechanika, illetve annak indeterminisztikus értelmezése azt állítja, hogy egy α-részecske kibocsátása nem tekinthető körülhatárolható, vagyis egyedi eseménynek, akkor voltaképpen nem tesz egyebet, minthogy szubatomi szintre vonatkoztat egy általános, és a filozófia által már korábban is megfogalmazott törvényszerűséget: az önazonosság hiányának általános törvényszerűségét. A magam részéről és így megközelítve tehát elfogadhatónak tartom az „indeterminizmust”.
Válasz erre 

Csebó Horváth János 2016.08.26. 14:08:33

Előző kommented alapján úgy látom, nem tudod eldönteni, hogy indeterminista legyél-e, vagy nem. Amiatt ugyanis, hogy az indeterminizmus ok nélkül enged be okozatot a létbe, nem tudod elfogadni, de amiatt, hogy Hérakleitoszhoz hasonlóan „végre” a fizikusok is megfogalmazták a fizikai entitások realitásának a hiányát, már szívesen elfogadnád. Márpedig az a helyzet, hogy ezt a két nézetet egyszerre kell elfogadni, vagy elvetni, mert ez ugyanannak a filozófiai nézetnek, az indeterminizmusnak a következménye.
A „fizikai realitás felszámolása” és az „oknélküliség megengedése” ugyanis egyszerre következik be akkor, amikor a határozatlansági relációt úgy értelmezik, hogy „nincs az elektronnak egy időben egyértelmű helye és sebessége”, így az „objektíven létező véletlenen” múlik, hogy a jövő egy pillanatában hol fog tartózkodni.
Erre persze mondhatod azt, hogy te az indeterminizmusból nem a fizikai realitás felszámolását, hanem egyenesen a fizikai entitások önazonosságának a felszámolását véled levezethetőnek, és a hogy a kettő nem ugyanaz. Valóban, a kettő nem ugyanaz, de a két különböző fogalmat, - az indeterministákkal együtt - te próbálod meg egymásba csúsztatni akkor, amikor a mikrorészecskék elmosódottnak látszó létezését a mikrorészecske önazonosság-hiányának bizonyítékaként állítod be.
Érdemes itt utalni arra, hogy ez az általánosítás az „Óramű” bejegyzésben jellemzett mechanisztikus indeterminizmushoz vezető extrapoláció tipikus esete: egy fizikai jelenség meg nem engedett ontológiai általánosítását hajtod végre. E meg nem engedett extrapoláció azért nem hajtható végre, mert a fizikai realitás felszámolása a mikrovilág jelenségeinek csak az egyik filozófiai interpretációjában jelenik meg, így a rá épített ontológiát is csak ezen interpretáció függvényeként, feltételesen fogalmazhatjuk meg. Tudatosan kerülni kellene azt a látszatot, miszerint „a kvantummechanika alátámasztja azt a filozófiai álláspontot, hogy a világ dolgainak nincs önazonossága, azok szubsztanciaként való felfogása nem lehetséges”. Azon túl, hogy ezt a tételt csak a filozófia kontextusában fogalmazhatjuk meg, a konkrét probléma az, hogy nem beszélhetünk úgy, mintha a mikrorészecskék „elmosódott létezése” a kvantummechanika egy megkérdőjelezhetetlen igazsága lenne. A valószínűségi értelmezést elutasítók a makro világ tárgyaihoz hasonlóan ugyanis továbbra is tulajdonítanak realitást a mikrofizikai entitásoknak, ők ugyanis feltételezik, hogy a részecskéknek vannak bizonyos, a méréstől függetlenül is meglévő tulajdonságai, és a mérés során ezek jutnak kifejeződésre. (Mint korábban már láttuk, az indeterministák szerint a mikrorészecskék ilyen objektív tulajdonságokkal nem rendelkeznek, a részecskék pontos helye, sebessége, energiája, stb. csak a mérés által {!} határozódik meg.) Bár, mint a bejegyzésben kifejtettem, a XX. században az indeterminista felfogás vált dominánssá, a rejtett paraméteres interpretáció mellett is nagyon erős érvek szólnak, így a helyzet korántsem egyértelmű, ezért a kvantummechanikára ontológiát alapozni csak feltételesen lehet.
De visszatérve a dolgok önazonosságára, nem kell ahhoz kvantummechanika, hogy az anyagi világ egyes entitásainak szubsztanciális mivoltát kétségbe vonjuk. Ezt elég meggyőzően megtehetjük a filozófia eszközeivel is: mivel minden dolog számtalan más dologgal van állandó kölcsönhatásban, így szigorúan nézve semminek sem lehet az időben két azonos állapota, akárcsak a Hérakleitosz által példaként felhozott folyónak.
Ugyanakkor úgy a hétköznapi életben, mint a fizikában folyton élünk azzal a feltevéssel, hogy a bennünket körülvevő tárgyak – gyakorlati értelemben – rendelkeznek bizonyos önazonossággal. A szobánkban lévő asztal például gyakorlati értelemben elég sokáig ugyanaz marad, miközben tudjuk, hogy Hérakleitosz folyójához hasonlóan állandó változásnak van kitéve: éri a napfény, ezért fakul; ha erősen megnyomjuk a lábát, akkor az kimozdul (gondoljunk a forgácslapból készült asztalokra); stb. A fizika ugyanígy, gyakorlati értelemben fogja fel az általa vizsgált dolgokat; egy biliárdgolyó önazonossága, amíg meg nem sérül, gyakorlatilag megmarad. Tehát a fizika soha nem tételezi fel az általa vizsgált entitások szubsztanciális mivoltát, (vagyis hogy minden változás során megmaradnának), megelégszik azzal, hogy egy adott kísérleti szituációban az adott tárgy rendelkezzen egy relatív önállósággal, tehát gyakorlati értelemben, az adott kontextusban legyen meg egy „bizonyos ideig tartó és egy bizonyos értelemben vett önazonossága”.

(Folytatása következik)
Válasz erre 

Csebó Horváth János 2016.08.26. 14:14:08

(Az előző komment folytatása)

A fizikus, amikor egy jelenséget megfigyel, fogalmi absztrakciókat (=elvonatkoztatásokat) hajt végre, az egyes összefüggőnek tűnő jelenségcsoportokat elválasztja végtelen hátterüktől, az így elkülönített „dolgok”-hoz bizonyos tulajdonságokat rendel, és a különböző tulajdonságú dolgok egymáshoz való viszonyaként értelmezi a jelenséget. Azt, hogy ezek a fogalmi absztrakciók mennyire relevánsak, a tapasztalat dönti el: ha az ezek segítségével megfogalmazott előrejelzéseinknek az újabb megfigyelések nem mondanak ellent, akkor használhatjuk őket. A fogalomalkotásnak, a „dolgok” megragadásának ez az absztrakció az alapja mind a makro-, mind a mikrovilágban. Emiatt tehát a „dolgok” éppen abban az értelemben vannak vagy nincsenek nagyban, mint kicsiben. A fizikai megismerésnek ezt a klasszikus felfogását képviselik ma is a rejtett paraméterek létezésében hívő kvantumfizikusok, de az indeterministák ezt némileg módosították.
Szerintük egy fizikai entitás, mint fentebb már láttuk, nem bír határozott, objektív tulajdonságokkal, ebből következően már a puszta létezése is kérdéses. Ahhoz ragaszkodnak, hogy a mikroszkopikus dolgokat empirikusan is megjelenítsék, de úgy fogják fel, hogy a mérés során a részecskére kapott fizikai mennyiségek csak a mérés által jönnek létre, ezek az értékek csak a mérés pillanatában jellemzik a részecskét, így mivel a mérés előtti és a mérés utáni állapotokról semmit nem mondanak, ezért a részecske egyes fizikai jellemzőiről csak valószínűségi kijelentést tehetünk. Úgy is felfoghatjuk ilyenkor a részecskét, mintha feloldódna a környezetében, és határozott állapotot majd csak egy újabb megfigyelés következtében kaphat. Arra a felvetésre, hogy ha ez így lenne, az Univerzum minden elemi részecskéjének megfigyeléséhez kellene egy megfigyelő, Wigner Jenő azt válaszolta, hogy ez a megfigyelő nem lehet más, csak az „Isteni tudat”, és hogy maga a kvantumelmélet egyenesen bizonyíték Isten létére. (Vö: hu.wikipedia.org/wiki/Schr%C3%B6dinger_macsk%C3%A1ja - sajnos forrás nélkül.)
Felfogása szerint „a »hullámcsomag redukciója« a kvantummechanika elméletében mint „deus ex machina” [isteni beavatkozás] jelenik meg, anélkül, hogy bármi kapcsolata volna az elmélet többi törvényével”. (Wigner Jenő válogatott írásai: Typotex, Budapest, 2005, 363.o.) (A hullámcsomag redukciója az indeterministák szerint az az esemény, amikor egy mikrorészecske a csak valószínűséggel leírható elmosódott állapotából a megfigyelés hatására egy határozott, fizikai mennyiségekkel jellemezhető állapotba kerül.) Bár minden tiszteletem Wigner Jenőé, e mellett mégsem tudok szó nélkül elmenni: igen nagy bajban lehet az a fizikai elmélet, amely valamely problémáját csak az isteni beavatkozással tudja megoldani. És ha valaki erre azt mondja, hogy Wigner Jenő véleménye nem lehet mérvadó a kvantummechnika elméleti kérdéseiben, az olvassa el az életrajzát: 1963-ban fizikai Nobel-díjat kapott az atommagok és az elemi részecskék elméletének továbbfejlesztéséért! (Vö: hu.wikipedia.org/wiki/Wigner_Jen%C5%91)
Válasz erre 

Birgi Zorgony 2016.08.28. 16:06:04

Igen, elismerem, hogy kissé problémás volt a múltkori eszmefuttatásom. Megpróbálom előbb tisztázni, helyesebben kialakítani álláspontomat a kérdésben, aztán pedig megpróbálok válaszolni a kritikai megjegyzéseidre.

Amit indeterminizmusként elfogadok és amit indeterminizmusként elutasítok, az két külön inde-terminizmus, és kétségtelenül adós maradtam e kettő egzakt megkülönböztetésével.

1. Kauzális indeterminizmus. Ahogy te megfogalmaztad, ennek lényege, hogy „ok nélkül enged be okozatot a létbe”. Itt tehát a szigorú kauzalitás felfüggesztéséről van szó: minden tényleges ok nélkül meg végbe valami. Ez szerintem joggal tekinthető a szó klasszikus értelmében csodának, azzal a megszorítással, hogy míg a klasszikus csodák irregulárisak, addig az efféle kvantummechanikai csodák éppen hogy regulárisak: olyan rendszerességgel történnek, hogy nem engedik be „maguk közé” a kauzalitást. Eszerint univerzumunk fundamentális „törvénye” kvantumfizikai szinten a csoda, vagy inkább a törvénytelenség. A helyzetnek ez az értelmezése nem véletlenül vezette el Wignert az általad is idézett megállapításhoz (a valószínűségi függvények az isteni tudat hatására „omlanak össze”).

2. Ontológiai indeterminizmus. Ennek lényegét Európában először Hérakleitosz fogalmazta meg: nem léphetünk kétszer ugyanabba a folyóba. Egyazon dolog folytonos változása másképpen megfogalmazva egy szakadatlan önazonosság-megtagadás. Ha ez a hérakleitoszi felfogás helytálló, s ha általános léttörvény (márpedig annak kell lennie, hiszen csupán annak a trivialitásnak sajátos megfogalmazása, hogy minden változik), akkor nemcsak a folyó van a permanens önazonosság-tagadás állapotában, hanem az elektron is. Ezt neveztem el az előző kommentben „ontológiai elmosódottságnak”. Itt nincsen szó kauzalitásról, illetve annak hiányáról, mint ahogy nincsen szó semmiféle természettörvény áthágásáról sem (mint a kauzális indeterminizmus esetében), mert ez a mikro- és makrovilág általános, természetes és szükségszerű sajátossága. Véleményem szerint erre a jelenségre ugyanúgy alkalmazható az „indeterminizmus” szó, mint a kauzális indeterminizmus jelenségére. A kauzális indeterminizmus esetében a meghatározatlanság a történések és változások véletlenszerűségében ölt testet, míg az ontológiai indeterminizmus esetében a változásnak alávetett „ontologikum” pontos létbeli meghatározatlanságában és meghatározhatatlanságában, folyamatos, már egyetlen időpillanatban is megvalósuló átmenetiségében ölt testet.

Két markánsan különböző jelenséggel állunk tehát szemben, amelyek nem függenek össze, követ-kezésképpen az egyik elutasítása minden további nélkül megengedi a másik elfogadását, és vice versa. Az egyik egy XX. századi természettudományos nóvum, a másik az ember évszázados, sőt évezredes tudásának része, illetve ennek a tudásnak egy sajátos interpretációja. Az ontológiai inde-terminizmus állításával tehát nem mondom ki a kauzális indeterminizmust, és vice versa.
Válasz erre 

Birgi Zorgony 2016.08.28. 16:08:09

Most akkor nézzük meg, hogy a kvantummechanikai indeterminizmus mit foglal magában, illetve hogy az indeterminizmus e két értelmezése közül melyikhez kapcsolódik.

Egy kvantummechanikai rendszer mérhető paramétereinek (helyzet, idő, energia, impulzus) való-színűségi eloszlása nem igényli a kauzális indeterminizmus feltételezését, hanem véleményem sze-rint sokkal jobban értelmezhető az ontológiai indeterminizmus keretei között. Tipikus példája ennek az atommag körül „keringő” valószínűségi függvény, vagyis a klasszikus fizika elektronja (mint elemi részecske). Az elektron paraméterei csak egy valószínűségi függvénnyel írhatók fel, vagyis az elemi részecskéből egy „elektronfelhő” lesz, de nem azért, mert ismeretlen erők hatnak rá, vagy mert mindenféle kauzális hatás nélkül is véletlenszerűen nyilvánul meg, hanem azért, mert van egy permanens ontológiai elmosódottsága – vagyis nem disztinkt. Szerintem az elemi részecskék méréstől függő részecske-, illetve hullámszerűsége úgyszintén értelmezhető az „ontoló-giai elmosódottsággal”, mert a részecske „valami”, a hullám pedig „megy valahová”, s mint az előző kommentben írtam, természetfilozófiai alapelv, hogy minden „valami” egyúttal „megy is valahová”. Voltaképpen minden leírható e két módon, vagyis állapotként és folyamatként. Az „ontológiai elmosódottságnak” azonban nyilvánvalóan megvannak a maga határai, vagyis egy elemi részecskét nem lehet akármennyire „elnyújtani” ontológiailag, és meghatározatlansága mindig meg fog maradni az adott valószínűségi függvény szélső értékei között. Bár az elektron pontos paraméterei meghatározatlanok lesznek, s így az felhőszerűen elmosódott valószínűségi függvénnyé változik, de ez a valószínűségi függvény szigorúan megmarad egy körpályán, s nem fog ad hoc kirándulásokat tenni a világban. És véleményem szerint pontosan ez mutatja, hogy itt nem egy kauzális indeterminizmussal állunk szemben, ebben az esetben ugyanis nem lehetne egy valószínűségi függvénnyel megragadni egy elemi részecskét, mert az véletlenszerűen és esetlegesen kitörne a valószínűségi függvény keretei közül. A hullámfüggvénynek ez a tulajdonképpen nagyon is szűk „játéktere” az, ami teljesen valószínűtlenné teszi a kvantummechanika kauzális értelemben vett indeterminisztikus értelmezését: abban ugyanis nem érvényesülhetne ilyen jellegű törvényszerűség.

Ad absurdum egy folyót vagy egy asztalt is csak valószínűségi függvény formájában lehet leírni, csak míg egy asztalban a sok ellentétes valószínűség statisztikailag kiegyenlíti egymást, s emiatt az csaknem disztinkt, addig egy elemi részecske – és minél „elemibb” a részecske, annál inkább – folytonos „átmenet”, vagyis ontológiailag fölöttébb bizonytalan és behatárolhatatlan. Ha egymilliárdszor feldobsz egy pénzérmét, akkor mérget vehetsz rá, hogy félmilliárd fej és félmilliárd írás lesz az eredmény (de ha lesz is a kettő között eltérés, az egészen elhanyagolható lesz), vagyis egy teljesen stabil eredményt fogsz kapni; míg ha csak egyszer dobsz fel egy pénzérmét, akkor az eredmény nagyon bizonytalan lesz, vagyis „statisztikailag” a két szélsőérték (fej vagy írás) valamelyike fog bekövetkezni. Ezért van az, hogy a mikrovilág szintjén az ontológiai elmosódottság sokkal jobban tetten érhető, mint a makrovilág szintjén.

Véleményem szerint a kvantummechanika határozatlansági jelenségeiért nagyrészt tehát az ontológiai indeterminizmus felelős, de ezekben a jelenségekben szerepe lehet annak is, ami első pillanatban és kellően felszínes megközelítésből kauzális indeterminizmusnak tűnik, de valójában ismeretlen hatások (vö. EPR-paradoxon) által determinált.

Szeretném tehát leszögezni: az ontológiai indeterminizmust mint a mindenség minden egyes elemének lényegi és természetes sajátosságát állítom, míg a kauzális indeterminizmust mint a mindenség bizonyos mikroelemeinek esetleges és természetellenes sajátosságát elutasítom.
Válasz erre 

Birgi Zorgony 2016.08.28. 16:15:13

A kritikád lényege az, hogy én ugyanúgy extrapolálom egy viszonylag szűk fizikai jelenségkör bizonytalan – indeterminisztikus – interpretációját a mindenség egészére, mint ahogy a szóban forgó kvantummechanikai értelmezés is megteszi ugyanezt, vagy ahogy korábban a mechanisztikus determinizmus is extrapolálta a mindenségre a maga fizikai törvényeit.

Amikor az „ontológiai elmosódottság” fogalmát összekapcsolom kvantummechanika egyes jelenségeivel, illetve az előbbi segítségével értelmezem az utóbbiakat, akkor kiindulópontom nem a kvantummechanika, hanem egy általános – hérakleitiánus – léttörvény. Nem egy partikuláris és bizonytalan tudományos elméletre építek egy univerzális törvényszerűséget, vagyis nem a fizika egy speciális területére vonatkozó elvet vonatkoztatok a mindenség egészére, hanem egy egyetemes hétköznapi tapasztalat filozófiai értelmezését vonatkoztatom a fizika specifikus területére, új és sokkal természetesebb értelmezését adva annak. A módszerem tehát nem induktív, hanem deduktív, nem természettudományos, hanem természetfilozófiai.

Számomra az önazonosság folytonos elveszítettségéből következő „ontológiai elmosódottság” egy értelmezési keret, amelyen belül a mikrorészecskékre vonatkozó valószínűségi hullámfüggvényt sokkal természetesebben lehet értelmezni (vö. Occam borotvája), mint a kauzális indeterminizmuson belül, s az indeterminizmus kauzális változata bizonyos értelemben úgy viszonyul ugyanennek ontológiai változatához, mint ahogy az arisztotelészi-ptolemaioszi epiciklus-elmélet viszonyul a brahei–kepleri ellipszis-teóriához.

+ + + + + +

Ha jól értelek téged és Wignert, akkor Wigner azt akarja mondani, hogy a valószínűségi függvények „összeomlasztásához”, vagyis ahhoz, hogy egy elemi részecske a maga „statisztikaiságából” átmenjen egy, a kvantummechanikai törvények által immár meghatározott állapotba, az kell, hogy legyen egy megfigyelője, s ez „kizárásos alapon” nem lehet más, csakis az isteni tudat. Érdekes felvetés, de tökéletesen egyetértek veled: „Igen nagy bajban lehet az a fizikai elmélet, amely valamely problémáját csak az isteni beavatkozással tudja megoldani.” Wigner következtetése szerintem sem tekinthető komolynak, éspedig – ahogy én látom – három okból:

1. Először is azért, mert erősen támaszkodik egy „ha”-ra, vagyis a kvantummechanika indeterminisztikus értelmezésére, s ekképpen egy bizonytalan dologból (a kvantummechanika indeterminista értelmezése) akar levezetni egy biztosat (Isten léte).

2. Másodszor azért, mert méltatlan helyzetbe hozza Istent. Ez a wigneri gondolat ugyanis Istent és a világ irányába megnyilvánuló isteni hatást alárendeli, vagy legalábbis szolgálatába állítja egy voltaképpen szubfizikai tényezőnek. A reguláris materialista felfogás a véletlent emelte fel isteni szint-re, és úgy vélekedett, hogy a véletlen az, ami létrehozza mindazt, amit korábban az isteni kreativitás művének tekintettek. Ezért mondják azt, hogy a véletlen a materialisták Istene. Wignernél ellenben arról van szó, hogy ő Istent állítja az indeterminizmusnak és a véletlennek a szolgálatába. Ez éppen ellentéte a fentinek: az előbbi álláspont a véletlent emelte fel Isten szintjére, Wigner álláspontja pedig Istent süllyeszti le a véletlen szintjére. Isten erre joggal mondhatná, hogy ő köszöni szépen, de nem kér ebből a „felemelő” feladatból, inkább megmarad a maga hagyományos elfoglaltságai mellett.

3. Végül pedig azért nem vehető komolyan Wigner következtetése, mert Istennek egy „antropomorf” értelmezéséből indul ki, amely szerint az isteni tudat a világ irányában úgy működik, mint egy emberi tudat. Isten és a világ viszonya azonban egyáltalán nem a szubjektumnak és az objektumnak az a viszonya, amely az ember esetében megjelenik, s amely – a kvantummechanika indeterminisztikus értelmezői szerint – a mérési szituációban beavatkozik az objektívnek hitt folyamatokba. Isten per definitionem fölötte áll az objektum–szubjektum dichotómiának, ha ugyanis nem állna fölötte e kettősségnek, akkor maga is része lenne a világnak, vagyis nem lenne Isten.
Válasz erre 

Csebó Horváth János 2016.08.31. 13:45:03

Úgy látom érdemes lenne rögzíteni a determinizmus és az indeterminizmus fogalmát, hogy ne beszéljünk el egymás mellett. Mivel azt gondolom, hogy az indeterminizmus a determinizmus tagadása, ezért a determinizmus fogalmából kell kiindulni.
A determinizmuson azt értjük, hogy „a fizikai világ egy bizonyos időpontban vett állapota a természeti törvényekkel együtt meghatározza a világ későbbi állapotait”. Ennek érvényessége két dolgon múlik: 1. van-e a fizikai világnak egyértelmű ontológiai állapota egy adott pillanatban 2. ha az első feltétel teljesül, akkor a fizikai törvények teljes ontológiai rendszere egyértelműen meghatározza-e a fizikai világ jövőbeni állapotait. Ha valamelyik feltétel nem teljesül, akkor a fizikai világ nem lehet determinista, tehát indeterminista.
Az első feltétel nem azt jelenti, hogy az ember meg tudja-e határozni, majd ezután le tudja-e írni a világ egy adott állapotát, hanem azt, hogy létezik-e egy egyértelmű állapota a világnak egy adott pillanatban. Ezen ontológiai adottság tehát független attól, hogy az ember milyen fogalmi rendszert alkot a világ leírására, az mennyire felel meg a tapasztalatainak, mennyire érvényesek azok az alapvető elvek és kategóriák, amelyekkel a maga körül tapasztalt világot próbálja megragadni. Azért mert ezen fogalmak, például maguknak a „dolgoknak” a fogalma olyan önazonossághiányt mutatnak, mint Herakleitosz folyója, a fizikai világ egészét mint egy összefüggő rendszert még jellemezheti az ontológiai egyértelműség. Másképpen fogalmazva, azért, mert a „dolgok”, mint önkényes emberi elvonatkoztatások eredményei híjával vannak a szubsztancialitásnak, a fizikai világ egésze még önálló szubsztanciaként felfogható. Ez persze már elvezet a dualizmus – monizmus filozófiai kérdéséhez, amivel itt most nem szeretnék foglalkozni, de tegyük fel, hogy a fizikai világ szubsztancialitásának problémája filozófialag megoldható. Ebben az esetben a „dolgok” ontológiainak látszó elmosódottságát „egyszerű” episztemológiai meghatározatlanságként foghatjuk fel, így a determinizmus első feltételét biztosíthatjuk, vagyis az általad „ontológiai indeterminizmus”-nak nevezett lehetőséget megkérdőjelezhetjük.
A második feltétel pedig a te „kauzális indeterminizmus” fogalmadnak felel meg, vagyis arról szól, hogy a fizikai törvények engedhetnek-e be új okozatot ok nélkül a létbe. Mivel korábban ezt a kérdést már elég jól körbejártuk, megegyezhetünk benne, hogy a determinizmusnak ez a feltétele teljesül.
Ezek után azt mondhatom, hogy egyetértek azzal, hogy a determinizmus teljesüléséhez mindkét feltétel szükséges, így ha valamelyik nem teljesül, akkor a világra az indeterminizmus jellemző. Egyetértünk abban is, hogy a második feltétel teljesül, de az első feltétellel kapcsolatban több ponton is eltér a véleményünk.
Egyrészt nem értünk egyet abban, hogy a világ ontológialag meghatározatlan lenne, szerintem a meghatározatlanság csak episztemológiai természetű. Másrészt nem értek egyet azzal, ahogy te, a legtöbb fizikai és ismeretterjesztői irodalom felfogását követve, a kvantummechanika indeterminista interpretációjára jellemző fogalmi leírást magának a mikrofizikai valóságnak a leírásának tekinted és levezethetőnek tartod a világra jellemző ontológiai indeterminizmusból.
Ezzel ugyanis megismétled azt az utat, amit Heisenbergék is bejártak: az indeterminista filozófiai alapállásuk következményeként született meg a kvantummechanika indetermista értelmezése. Nem győzöm hangsúlyozni, hogy a mikrovilágnak az általad leírt képe csak az egyik lehetséges modell valóságképe, de nem maga a „valóság”. Mint már korábban említettem, például a Bohm-mechanika teljesen más valóságképet fest fel ugyanarról a valóságról, olyat, amely a te ontológiai indeterminizmusoddal nem egyeztethető össze. És ha egyszer elkészül egy reális-lokális-determinista leírás is (ami minden korábbi no-go tétel ellenére lehetséges, vö: E.Szabó, 198.o.), az is teljesen más valóságképet fog eredményezni, méghozzá olyat, amely az ontológiai indeterminizmussal szintén nem lesz összhangban.
(Folyt.köv)
Válasz erre 

Csebó Horváth János 2016.08.31. 14:12:50

(Az előző folytatása)

Egyébként Heisenberg indeterminizmusa nem csak a kauzalitás elvetésében jelentkezett, hanem – amint az alábbi idézetből is látszik – a determinizmus másik feltételének a lehetőségét is tagadta: „Kant nyilván nem láthatta előre, hogy egy, a hétköznapi tapasztalatok világától olyannyira távol eső kísérleti birodalomban nem bánhatunk majd úgy a megfigyelésekkel, mintha továbbra is megfelelnének a »Ding an sich« vagy a tárgyak kritériumának, azaz nem láthatta előre, hogy az atom nem dolog vagy tárgy.” (Heisenberg: Rész és egész) (Ez még jobban aláhúzza azt a bejegyzésben már leírt véleményemet, hogy Heisenberg már indeterministaként közeledett a mikrofizikai tapasztalatokhoz, és ez eredményezte a kvantummechanika indeterminista értelmezését.) Azonban azóta már tudjuk, hogy az atom dologként való felfogásának a priori elutasítása nem az egyetlen útja a mikrovilág leírásának,mert a Bohm mechanika megmutatta, hogy igenis meg lehet tartani az elemi részek „dologi absztrakcióját”, érvényességéről csak a leírás eredményessége dönthet, ez pedig csak a tapasztalat során dőlhet el.
Úgy tűnik, hogy az eltérő filozófiai prekoncepciók eltérő a priori döntéseket eredményeznek a fizikai elmélet fogalmi rendszerére vonatkozóan, de a különböző fogalmi struktúrák a hozzájuk tartozó különböző fizikai tartalommal együtt eredményezhetnek egymással ekvivalens leírásokat abban az értelemben, hogy a tapasztalatokkal mindegyik összhangban van, és ugyanazokat az előrejelzéseket adja. Ugyanakkor az eltérő fogalmi rendszer mindig eltérő valóságképet indukál. Vegyük a következő sémát:

filozófia ---> fogalmi struktúra ---> valóságkép
+++++++++++ fizikai tartalom
=======================
------------------- fizikai elmélet <--- ---> kísérleti tapasztalat

Vagyis:
1. A fizikus filozófiai meggyőződése meghatároz egy fogalmi struktúrát, amivel megpróbálja megragadni a vizsgált fizikai valóságot, ami a fizikai tartalomtól függetlenül már meghatároz egy valóságképet.
2. A fogalmi struktúra alkalmazásával vizsgálja a fizikai valóságot, ezen fogalmakkal ragadja meg az adott fizikai tartalmat. Így áll elő a fizikai elmélet.
3. A fizikai elmélet előrejelzéseit összeveti a kísérleti tapasztalatokkal.
Ezt a sémát látjuk megvalósulni úgy a kvantummechanika, mint a relativitáselmélet létrejöttekor.

Ilyenkor vajon mi alapján döntsünk az egymással ekvivalens fizikai elméletek között. Úgy látszik, te a filozófiát tekinted elsődlegesnek, én a valóságképet, a fizikusok egy része pedig a fizikai elmélet szépsége, egyszerűsége alapján dönt. Hogyan lehetne ettől a relativizmustól megszabadulni?
Válasz erre 

Birgi Zorgony 2016.09.06. 16:24:47

Előző hozzászólásomban kiindulópontom Hérakleitosz triviális megállapítása volt, mellyel alighanem mindenki egyetért: kétszer nem lehet ugyanabba a folyóba lépni. Magától értetődően ez azt is magában foglalja, hogy kétszer ugyanarra az asztalra sem lehet rákönyökölni. Ez az axióma két dolgot mond ki:

1. Minden szakadatlanul változik. Hérakleitosz kijelentésének ez a triviális része, mert kimondja azt, amit mindenki tud: minden „mozog”, vagyis minden a folytonos módosulás állapotában van. Ez nemcsak a világ egyes elemeire – folyó, asztal, elektron stb. – igaz, hanem annak egészére is: nem lehet kétszer ugyanabba a világba „lépni”.

2. Ezen túl azonban e kijelentés magában foglal valamit, ami már korántsem annyira triviális: minden, ami változik, „megmásul”, s így folyamatosan elveszíti önmagával való azonosságát. Ez a folyamatos önazonosságvesztés a hérakleitoszi kijelentés hétköznapi olvasatának természetfilozófiai implikációja. Ettől a folytonos „megmásulástól” az adott dolog még ugyanúgy létezik, mint korábban, de ami létezik, az már nem ugyanaz. Ezt jelenti a permanens megmásulás, a folyamatos önazonosságvesztés – ami persze csak egy másik megfogalmazása annak a triviális igazságnak, hogy minden változik.

Most akkor vizsgáljuk meg, hogyan viszonyul Kratülosz kijelentése Hérakleitoszéhoz. Kratülosz azt mondja: már egyszer sem lehet ugyanabba a folyóba lépni. Ez azt jelenti, hogy egy adott dolog „ugyanazonsága” avagy önazonossága nemcsak két pillanat relációjában illuzórikus, hanem már egyetlen pillanat vonatkozásában is az: nem lehet hiteles „pillanatfelvételt” készíteni semmiről.

Hérakleitosz tehát azt mondja, hogy ha egyszer belépünk a folyóba, majd utána még egyszer, akkor az már nem ugyanaz a folyó lesz. A két belépési időpont közötti intervallum azonban minden határ nélkül osztható. Ez pedig azt jelenti, hogy nincs egyetlen megragadható pillanat sem, amelyben a folyó ugyanazonsága teljesülhetne, mert minden „pillanatról” kiderül, hogy intervallum, vagyis tovább osztható. Az a pillanat, amely nem intervallum, ezzel szemben csupán hipotetikus, mert kívül van az időn. Egy folyó ugyanazonsága tehát csak az időn kívül valósulhat meg. Időbeli ugyanazonság nincs.

De ellenkező oldalról közelítve is ugyanide jutunk. Ha ugyanis volna olyan pillanat, amelyben megvalósulna egy folyó önazonossága, akkor ennek az önazonosságnak a következő pillanatban is fenn kellene állnia, merthogy nem lehetséges, hogy egy folyó váltakozva állandó legyen és változzon. Ami változatlan, vagyis önmagával minden tekintetben azonos, annak ezt követően is változatlannak kell maradnia; ha viszont változik, nem képzelhető el, hogy legyenek olyan pillanatai, amikor változatlan. Ha tehát nem lenne igaza Kratülosznak, akkor a folyó vagy nem folyna – vagyis változatlan lenne –, vagy ami még rosszabb, állandóan megindulna és megtorpanna. Hérakleitosz elfogadása Kratülosz elutasítása mellett tehát szükségképpen vezet egy „döcögős világ”-hipotéziséhez.

A permanens változás világából még egy pillanat vonatkozásában sem emelhető ki az állandóság és az ugyanazonság. Ennek legfeljebb csak annyi teoretikus – vagy inkább hipotetikus – lehetősége lehet, mint magának az időpillanatnak. Ami kontinuus, az nem „kvantálható” a szó szigorú értelmében, vagyis nem tehető diszkontinuussá. A kontinuitás nem házasítható össze a diszkontinuitással.

Mindebből pedig az következik, hogy a világ nem rendelkezik egy tökéletesen behatárolható ontológiai állapottal, mert a folytonos átmenet állapotában van, mind részeiben, mind egészében, akár van erről tudomása a tudománynak, akár nincs. Ez nem természettudományos, hanem természetfilozófiai teoréma, mely Hérakleitosz axiómájából szükségképpeni módon következik. És a fix ontológiai állapotot nemcsak gyakorlati, de elvi értelemben sem lehet „detektálni”.

Ha van stabil – önazonos – ontológiai állapota a világnak, akkor csak az van neki, s nincsenek átmenetek, vagyis nincs változás; ha van ontológiai átmenete a világnak, akkor csak az van neki, s nincs stabil állapota még egyetlen pillanat vonatkozásában sem. A kettőt nem lehet összeházasítani: nem lehet egyszerre ragaszkodni a változáshoz („megy valahová”) és a léthez („valami”). Ami „megy valahová”, az sosem lesz valami; ami „valami”, az sosem fog menni valahová.

A platóni értelemben vett „keletkezés” egy pillanatra sem lesz platóni értelemben vett „lét”, hanem mindig is csak keletkezés, levés, létesülés marad, vagyis a keletkezés világa nemcsak egy intervallum („kétszer nem lehet ugyanabba...”), hanem már egy pillanat vonatkozásában sem („egyszer sem lehet ugyanabba...”) mutatja jeleit az állandóságnak, vagyis a létnek.
Válasz erre 

Birgi Zorgony 2016.09.06. 16:27:25

Nézzük akkor most újra az indeterminizmus változatait, hogy világos legyen, mi a különbség aközött, amit fentebb kifejtettem, és aközött, amit a tudomány képvisel, illetve ezek miben azonosak. A korábbi hozzászólásomban két változatát említettem az indeterminizmusnak, most azonban ezt kibővítem egy újabbal:

1. Ontológiai indeterminizmus. Ennek jelentéstartalmát most fejtettem ki. Jómagam ezt az álláspontot osztom.

2. Kauzális indeterminizmus. Bizonyos „okozatok” ok nélkül jelennek meg. Véleményem szerint elfogadhatatlan, mert állandósítja a csodát, s ellentmond a megmaradási törvényeknek csakúgy, mint a kauzalitás univerzális elvének.

3. Valószínűségi indeterminizmus. Mindaddig, amíg a szubjektum nem avatkozik be megfigyelése révén bizonyos objektív kvantumfizikai folyamatokba, addig azok léte csupán valószínűségi természetű, és ez a valószínűség csak a beavatkozás (mérés, vizsgálódás) hatására szűnik meg, vagyis például csak a beavatkozás hatására lesz egy „elektronfelhőből” – az elektronból mint hullámból – elektron-korpuszkula. Jól láthatóan e harmadik indeterminizmus is ontológiai természetű, akárcsak az első.

Nézzük meg azonban most azt is, hogy mi a különbség az indeterminizmus 1. és 3. változata között.

1. Az ontológiai indeterminizmus egyetemes jelenség, mind a mikro-, mind a makrovilágra jellemző, míg a valószínűségi indeterminizmus csak a mikrovilág vonatkozásában vetődik fel, és megoldatlan, miért csak ebben a vonatkozásban vetődik fel.

2. Az ontológiai indeterminizmus állapotából a tárgyak sosem lépnek ki. A valószínűségi indeterminizmus „időszakos” természetű: a determinizmus (vö. „a hullámfüggvény összeomlása”) és az indeterminizmus állandóan váltakozik benne; a vizsgált dolgok hol kilépnek a determinizmus világából, hol újra visszalépnek.

3. Az ontológiai indeterminizmus értelmében a megfigyelés semmiféle ontológiai hatással nincs a tárgyakra. A valószínűségi indeterminizmus értelmében a megfigyelés jelenléte vagy hiánya alapjában változtatja meg a megfigyelt objektumot.

4. Az ontológiai indeterminizmus évezredes tudása az embernek, s ha Nyugaton nem is vált általánosan elfogadottá, Távol-Keleten – különösen az ind védánta-bölcseletben – lényegi eleme a valóság-értelmezésnek. Ezzel szemben a valószínűségi determinizmus XX. századi természettudományos hipotézis.

Remélem, sikerült világossá tennem, mi az álláspontom, illetve az miben különbözik az indeterminista tudományos állásponttól, bármilyen értelemben is fogjuk fel e tudományos indeterminizmust. Remélhetőleg az is világos, hogy a világ kontinuus voltából fakadó „ontológiai elmosódottsága” semmilyen módon nem „véletlenszerűsíti” a világot, csupán – à la Kratülosz – nem engedi a világ-kontinuum „diszkontinualizálását” még egyetlen pillanat vonatkozásában sem. Ugyanakkor a dolgok „ontológiai elmosódottsága” kiválóan alkalmas arra, hogy magyarázatául szolgáljon ama kvantumfizikai jelenségek legalábbis egy részének, amelyek tudományos – „koppenhágai” – magyarázatai ellentmondanak mind a kipróbált és bevált tudományos törvényeknek, mind a természetfilozófiai „józan észnek”.
Válasz erre 

Birgi Zorgony 2016.09.06. 16:30:12

Néhány konkrét megjegyzésedre szeretnék még reflektálni.

1. Az egyik „elbeszélési pontunk” érzésem szerint az, hogy te a folyamatos változást determinizmusként értelmezed, mert hisz éppen egy kauzális összefüggésrendszer az, aminek hatására az adott dolog változáson megy át. Ezzel maradéktalanul egyetértek. Én azonban másképpen és máshonnan ragadom meg a kérdést: az adott dolog – a folytonos determinációk hatására – folyamatos ontológiai átmenetben, vagyis az „ontológiai elmosódottság” – a platóni keletkezés – állapotában van. Ha úgy tetszik, alkalmazhatjuk erre a „determinált indeterminizmus” kifejezést is.

2. Azt írod: „Azért mert ezen fogalmak, például maguknak a »dolgoknak« a fogalma olyan önazonossághiányt mutatnak, mint Herakleitosz folyója, a fizikai világ egészét mint egy összefüggő rendszert még jellemezheti az ontológiai egyértelműség.” Ez nem így van, és ezzel kapcsolatban csak arra tudok gondolni, hogy nem értetted meg, hogy a folytonos „önazonosságvesztés” csupán egy másik megfogalmazása annak, hogy „változás”. Te ugyanis azt állítod, hogy lehet, hogy a világban minden alá van vetve a változásnak, de a világ egésze nincs alávetve. Ez pedig nonszensz.

3. Azt írod: „Nem értek egyet azzal, ahogy te, a legtöbb fizikai és ismeretterjesztői irodalom felfogását követve, a kvantummechanika indeterminista interpretációjára jellemző fogalmi leírást magának a mikrofizikai valóságnak a leírásának tekinted, és levezethetőnek tartod a világra jellemző ontológiai indeterminizmusból. Ezzel ugyanis megismétled azt az utat, amit Heisenbergék is bejártak: az indeterminista filozófiai alapállásuk következményeként született meg a kvantummechanika indeterminista értelmezése.” Ezzel szemben én nem „a kvantummechanika indeterminista interpretációjára jellemző fogalmi leírást” tekintem – természetesen csak relatív – kiindulópontnak, hanem azt a jelenséget – mondhatni kísérleti tapasztalatot –, amelynek ez a leírás az egyik, szerintem helytelen értelmezése, s amely helyett jómagam egy másik értelmezést kíséreltem meg. Továbbá, ha egyszer a „koppenhágaiak” indeterminista kvantumfizika-értelmezése és az én értelmezési kísérletem között – mint fentebb bemutattam – nehezen eltúlozható a különbség, akkor nyilván az általános „koppenhágai” indeterminista háttérszemlélet és az én indeterminista háttérszemléletem között is meg fog jelenni ugyanez a különbség. Ahogy a két kvantummechanikai értelmezés összemosása illegitim részedről, éppoly illegitim a két indeterminisztikus háttérszemlélet összemosása.

4. Azt írod: „Úgy látszik, te a filozófiát tekinted elsődlegesnek, én a valóságképet, a fizikusok egy része pedig a fizikai elmélet szépsége, egyszerűsége alapján dönt. Hogyan lehetne ettől a relativizmustól megszabadulni?” A valóságképet elsődlegesnek tekinteni filozófia nélkül csak a naiv realizmus tudja. Viszont a naiv realizmus is filozófia: mindennemű filozófiai megfontolás elutasításának „filozófiája”. Amikor a valóságképet tekinted elsődlegesnek, neked is megvannak a filozófiai előfeltevéseid, és te is a saját valóságképedből indulsz ki. Gondolj csak Karácsony Rezső „Egy a valóság s ezer a ruhája” című háromkötetes, többször is kiadott fizikai olvasókönyvére! A cím azonban eredetileg Szabó Lőrinc „Ez vagy te!” című versének egy sora, s minthogy ez utóbbi a Csándógja upanisad egyik részletének költői átirata, a könyv és a vers valóságfelfogása homlokegyenest ellentétes egymással: az előbbinél az egyetlen valóság a fizikai univerzum, az anyag, az utóbbinál Isten. A fizikának is megvannak a maga filozófiai előfeltevései, még akkor is, ha a természettudósok rendszerint botcsinálta filozófusok (például az általad közölt idézetben Heisenberg összetéveszti a kanti Ding an sichet, vagyis a numenont a fenomenonnal). Egy fizikai elmélet szépsége szerintem az általános tudományos világképet sosem fogja meghatározni, legfeljebb egy-egy részletprobléma megoldását befolyásolhatja. Tehát marad a filozófiai-szubfilozófiai-ideológiai előfeltevés, viszont ez megkerülhetetlen. Mindaz, aminek következtetésként van filozófiai jelentősége, szükségképpen filozófiai premisszákból származik, ráadásul a filozófiai input szükségképpen összhangban is lesz a filozófiai outputtal. Ami például a modern természettudományt legáltalánosabb filozófiai nézetként meghatározza, az az, hogy az egész a részekből jön létre. Ezért a modern természettudomány módszertanilag analitikus, és ebből nagyon sok minden levezethető. Egy, a részeket az egész elé helyező tudományos szemlélet nem lehet, hogy ne legyen analitikus, nem lehet, hogy ne legyen materialista, és nem lehet, hogy ne legyen evolucionista.

Ami pedig a különböző előfeltevésekből fakadó „relativizmust” illeti, ezt talán az tudja legjobban elkerülni, aki képes reflektálni saját előfeltevéseire, s ugyanakkor – szinoptikus módon – kívülről és felülről képes rátekinteni a különböző szempontokra.
Válasz erre 

Csebó Horváth János 2016.09.11. 21:13:33

Mivel a véleményemet lényégében már kifejtettem korábban, itt már csak néhány konkrét megjegyzésedre szeretnék reflektálni.

1. Ezt írod: „Ha van stabil – önazonos – ontológiai állapota a világnak, akkor csak az van neki, s nincsenek átmenetek, vagyis nincs változás; ha van ontológiai átmenete a világnak, akkor csak az van neki, s nincs stabil állapota még egyetlen pillanat vonatkozásában sem. A kettőt nem lehet összeházasítani: nem lehet egyszerre ragaszkodni a változáshoz (»megy valahová«) és a léthez (»valami«). Ami »megy valahová«, az sosem lesz valami; ami »valami«, az sosem fog menni valahová. A platóni értelemben vett „keletkezés” egy pillanatra sem lesz platóni értelemben vett „lét”, hanem mindig is csak keletkezés, levés, létesülés marad, vagyis a keletkezés világa nemcsak egy intervallum („kétszer nem lehet ugyanabba...”), hanem már egy pillanat vonatkozásában sem („egyszer sem lehet ugyanabba...”) mutatja jeleit az állandóságnak, vagyis a létnek.”

Elismerem, hogy a determinizmussal kapcsolatban joggal felvethető a „lét és a változás filozófiai problémája”, de nem fogadom el, hogy ez a két, komplementernek látszó fogalom filozófiailag ne lenne összeegyeztethető valahogy ahhoz hasonlóan, ahogy azt a fizika megtette. A két fogalom együttes fennállásának tagadása a következőt jelenti:
a. Van lét, de nincs változás: ez ellenkezik a legelemibb tapasztalatainkkal.
b. Van változás, de nincs lét: mi változik, ha nincs ami változzon?

A problémát a fizikában Zénon egyik paradoxona így fogalmazza meg: „Egy repülő nyílvesszőt kell elképzelnünk. Bármely időpillanatban a nyíl a levegő egy ismert pontján tartózkodik. Ha ennek a pillanatnak nincs időbeli kiterjedése, akkor a nyílnak »nincs ideje«, hogy elmozduljon, tehát nyugalomban kell, hogy legyen. Hasonló logikával belátható, hogy az ezt követő pillanatokban is nyugalomban van. Mivel ez az idő bármelyik pillanatára igazolható, a nyílvessző egyáltalán nem mozoghat: a mozgása csak illúzió.”
(Vö: hu.wikipedia.org/wiki/Z%C3%A9n%C3%B3n_paradoxonjai)

E paradoxon ugye azt állítja, hogy van lét, de nincs változás. A fizikában ezt az ellentmondást úgy oldjuk fel, hogy a nyílvessző létét nem egy, hanem két paraméterrel jellemezzük: a hely-paraméter megadja, hogy egy adott időpillanatban hol van, a sebesség-paraméter pedig, hogy a következő idő pillanatokban hol lesz. Tudjuk jól, hogy az állapotjellemzés ezen módja a mechanikai mozgások esetében teljesen kielégítőnek bizonyult, ez alapján tudjuk előre jelezni a bolygók helyzetét éppúgy, mint a rakétákét.

Szerintem elvileg nincs semmi akadálya annak, hogy Laplace démonja tudjon készíteni egy pillanatfelvételt a világ „összes nyílvesszőjéről”, vagyis számba vegye minden egyes fizikai entitás állapotjellemző paramétereit, és mindazokat a kölcsönhatásokat, amelyek az egyes entitások állapotváltozásait okozhatják, majd ezen adatokból kiszámolja, hogy a jövő egy tetszőleges pillanatában milyen állapotban lesznek. Ez az előrejelzés természetesen arra is képes lehet, hogy egyes entitások megszűnését, pontosabban másokba való feloldódását leírja. Tehát az egyes entitások létének időbeli állandósága nem feltétele ezen előrejelzésnek, elegendő egy olyan relatív elkülönültség, amely az állapotfelmérés pillanatában fenn áll. Így szerintem az általad hangsúlyozott ontológiai indeterminizmus nem létezik, ez csak egy „egyszerű” episztemológiai probléma ontológiai méretűvé való felnagyítása. Természetesen ezt az ismeretelméleti problémát, vagyis a fizikai világ egy kezdeti állapota meghatározását, az ember soha nem lesz képes megoldani, de ez nem jelenti azt, hogy mindegy lenne, hogy milyen természetű oka lehet a probléma megoldhatatlanságának: ontológiai vagy episztemológiai?
Válasz erre 

Csebó Horváth János 2016.09.11. 21:18:11

(Az előző folytatása)

2., Ezt írod: „Az egyik »elbeszélési pontunk« érzésem szerint az, hogy te a folyamatos változást determinizmusként értelmezed, mert hisz éppen egy kauzális összefüggésrendszer az, aminek hatására az adott dolog változáson megy át. Ezzel maradéktalanul egyetértek. Én azonban másképpen és máshonnan ragadom meg a kérdést: az adott dolog – a folytonos determinációk hatására – folyamatos ontológiai átmenetben, vagyis az »ontológiai elmosódottság« – a platóni keletkezés – állapotában van. Ha úgy tetszik, alkalmazhatjuk erre a »determinált indeterminizmus« kifejezést is.”

Ezek alapján úgy látszik, hogy szerinted a fizikai világot végső soron az indeterminizmus jellemzi, a »determinált indeterminizmus« kategóriája úgy tűnik, csak játék szavakkal. Nem látszik, hogy mire vonatkozhatna az általad elfogadott oksági determinizmus, ha egyszer tagadod bárminek a határozott létezését, ami a tárgya lehetne ennek a determinizmusnak. Ha nem lenne ontológiailag meghatározott a világ, akkor az vajon nem azt jelentené, hogy helyből feltételezünk a létben olyan okozatokat, amelyek mögé semmilyen oksági rendszert nem tudunk rendelni?
Én úgy látom, hogy megpróbáltad itt összeegyeztetni Arisztotelész szigorú oksági rendszerét és Platón ontológiai indeterminizmusát, de szerintem ez nem sikerült.

3., Egyébként szerény filozófiai ismereteim szerint legutóbb Whitehead próbálta meg az általad hangsúlyozott „lét és változás” filozófiai problémájának a megoldását. Azt nem tudom, hogy milyen sikerrel, de lehetségesnek tartom, hogy sikerült oldania azon a kibékíthetetlen ellentéten, ahogyan te Platónt követve interpretáltad a kérdést.
Válasz erre 

Birgi Zorgony 2016.09.14. 23:17:57

Kritikád lényegi pontokra mutat rá, de ezek kifejtése már túlmutat a jelenlegi bejegyzésen. Úgyhogy csak rövid utalásokra vállalkozom.

A Zénón-paradoxonok ugyanarra világítanak rá, amit én is megpróbáltam elmondani: a kontinuus „mennyiségek” diszkontinuizálása – megszakítása, „kvantálása” – önellentmondásokba torkollik. Ha felveszünk egy diszkrét állapotot, akkor abból már sosem lesz mozgás. A megoldás, amit javasoltál (a nyílvesszőnek adott sebesség-paraméter) a megoldás illegitim belecsempészése magába a problémába, ugyanis a sebességhez idő is kell, márpedig a pillanat lényege az idő hiánya. Laplace démonjának pillanatfelvételében sem lesz benne a sebesség. Te legfeljebb csak két pillanat relációjában vehetsz fel sebességet (amihez persze két térbeli pont relációja is szükséges), viszont ezzel vissza is kerültünk a Zénón-paradoxonhoz, vagyis nem oldottunk meg semmit. Ha a mozgást akarjuk, el kell utasítanunk a pillanatnyi állandóságot is; ha ragaszkodunk hozzá, nem tudunk megmozdulni.

Attól tartok, amikor én létről beszélek, szemben a változással, akkor te a „lét” alatt az anyagi univerzum létére gondolsz. Amiről viszont én beszélek, az a platóni értelemben vett lét, melynek lényege a változatlanság (önazonosság). Az anyagi univerzum – a platóni értelemben vett keletkezés – lényege viszont a változás (permanens önazonosságvesztés). Direkt módon Kratülosz (egyszer sem lehet ugyanabba a folyóba lépni), indirekt módon pedig Zénón (a nyílvessző egyetlen pillanatban sem lehet nyugalomban, mert az lehetetlenné tenné a mozgást) mutatott rá arra, hogy a fizikai univerzumnak pillanatnyi vonatkozásban sincs önazonos léte.

Az a helyzet, hogy az általad felvetett „a” és „b” verziót egyaránt helytállónak találom, csak más vonatkozásban. Egyrészt az, hogy „van lét, de nincs változás”, a lét platóni definíciójának lényege, mert hiszen a lét mindig önazonos, s így kizárja a változást. A lét per definitionem változatlan. Ettől lét. A „lét” azonban nem az anyagi univerzumot jelenti, hanem az ideák világát, végső soron és legteljesebb értelemben pedig az isteni létet. Úgyszintén helytálló az, hogy „van változás, de nincs lét”, csak immár a keletkezés világának, vagyis a mi empirikus világunknak a vonatkozásában. „Mi változik, ha nincs, ami változzon?” – teszed fel a kérdést. Jó kérdés, de én is feltehetném neked: Mi lenne az, ami változik? Persze, az anyag változik. Na de mi az anyag? Az anyagot mi csak változásként, s nem létként ismerjük. Semmi nem tudunk arról, mi az anyag szubsztanciája. Skolasztikus – és paradox – megfogalmazással élve mit sem tudunk az anyag materiájáról, csak különböző (megjelenési) formáit ismerjük. Az atomokról kiderült, hogy nem atomoszok, az elemi részecskékről, hogy nem elementariusok, a kvarkoknak meg „színeik” vannak. A materia – a valódi, a tiszta anyag – hajszája a formák áradatában tehát tovább folyik. A Wikipédia „Elemi részecske” szócikke ugyanezt így fogalmazza meg: „A fizika egyik leglényegesebb célkitűzése, hogy megtalálja a legelemibb részecskéket, amelyekből az összes többi részecske felépíthető, míg maguknak nincsenek még elemibb összetevőik.” Ilyet azonban nemcsak gyakorlatilag, de elvileg sem lehet találni, mert minden változás elemi fundamentumának, annak, ami mindenben ugyanaz, változatlannak kellene lennie. Ámde ha lenne ilyen, akkor – à la Zénón – megint csak nem lenne változás. A formák – kvalitás-együttesek – áramlása mögött nincs semmi szubsztancialitás. Van tehát változás, de nincs változó. Ha a változás mögött volna változó, akkor az változatlan volna. Csak a változás változik.

Azt írod: „Nem látszik, hogy mire vonatkozhatna az általad elfogadott oksági determinizmus, ha egyszer tagadod bárminek a határozott létezését, ami a tárgya lehetne ennek a determinizmusnak.” Az okság, ha jól megnézed, nem a létezéshez mint olyanhoz, hanem a változáshoz mint olyanhoz kapcsolódik. Az okság még az álomban is működik, ahol van változás, viszont nincs, ami változna. Okság és változás elválaszthatatlanok; nincs változás okság nélkül, nincs okság változás nélkül. A kettő egyazon érem két oldala. A mozgás és változás elidegeníthetetlen sajátossága a folytonos – kratüloszi értelemben szakadatlan, „indiszkrét” – átmenetiség. Azért, mert valaminek nincs diszkrét állapota, miért ne vonatkozhatna rá az okság? Miért tagadná ez a permanens ontológiai átmenetiség az okságot? Éppen hogy feltételezi! De természetesen maga a kauzalitás is kontinuus. Kauzális determinizmus és folytonos változás (ontológiai átmenetiség): ezek elválaszthatatlanul összetartoznak.

Összefoglalva, egyetértek veled a kvantummechanika koppenhágai értelmezéséből kiinduló kauzális és valószínűségi indeterminizmus elutasításában, de a klasszikus természetfilozófiából kiindulva felvetem az „ontológiai indeterminizmus”, illetve az „ontológiai elmosódottság” fogalmát – amely viszont egyszerűen annyit jelent, hogy a változás nem ismer diszkrét állapotot: egyszer sem léphetünk ugyanabba a folyóba.
Válasz erre 
süti beállítások módosítása